In a rectangle ABCD, points X and Y are the midpoints of AD and DC, respectively. Lines BX and CD when extended intersect at E, lines BY and AD when extended intersect at F. If the area of ABCD is 60 then the area of BEF is
60
80
90
120
The correct Answer is:C
Step by step video, text & image solution for In a rectangle ABCD, points X and Y are the midpoints of AD and DC, respectively. Lines BX and CD when extended intersect at E, lines BY and AD when extended intersect at F. If the area of ABCD is 60 then the area of BEF is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II (MATHEMATICS)
5 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-I ( MATHEMATICS)
20 Videos
- MOCK TEST 9BOOK - KVPY PREVIOUS YEARCHAPTER - MOCK TEST 9EXERCISE - EXERCISE
25 Videos
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-II(MATHEMATICS)
10 Videos
Similar Questions
Knowledge Check
In the figure, ABCD is a square. E and Fare midpoints of AD and BC respectively. The ratio of areas of ΔGAB and ΔHAB
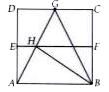 A4 : 1B1 : 4C1 : 2D2 : 1
A4 : 1B1 : 4C1 : 2D2 : 1ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2ABCD is cyclic quadrilateral. Sides AB and DC, when produced , meet at E and sides BC and AD, when produced, meet at F. If ∠BFA=60∘ and ∠AED=30∘ , then the measure of ∠ABC is :
AA)75∘BB)65∘CC)80∘DD)70∘
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH.
View SolutionABCD is a rectangle and E F G and H are the mid-points of AB BC CD DA respectively Prove that EFGH is a rhombus
View SolutionABCD is a parallelogram. P and R are the midpoints of DC and BC respectively. The line PR intersects the diagonal AC at Q . The distance CQ will be equal to
View SolutionIn the given figure, if ABCD is a rectangle and P, Q are the mid-points of AD, DC respectively. then, the ratio of lengths PQ and AC is equal to
View SolutionABCD is a rectangle and E and F are the mid-points of AD and DC respectively. Then the ratio of the areas of EDF and AEFC would be (a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 2 : 3
View Solution

