ABCD is a parallelogram. P and R are the midpoints of DC and BC respectively. The line PR intersects the diagonal AC at Q . The distance CQ will be equal to
AC4
BD3
BD4
AC3
To solve the problem, we need to find the distance CQ in the given parallelogram ABCD where P and R are the midpoints of sides DC and BC respectively, and line PR intersects diagonal AC at point Q.
1. Identify Points and Midpoints:
- Let A,B,C,D be the vertices of the parallelogram ABCD.
- P is the midpoint of DC.
- R is the midpoint of BC.
2. Draw the Diagonal:
- Draw diagonal AC in the parallelogram.
3. Join Points:
- Join points P and R to form line PR.
- This line intersects diagonal AC at point Q.
4. Use Similar Triangles:
- In triangle CQR and triangle COB (where O is the midpoint of diagonal AC):
- CQ is a side in triangle CQR.
- CR is half of CB since R is the midpoint of BC.
- Let CB=2x, then CR=x and CQ=y.
5. Set Up Ratios:
- By the properties of similar triangles:
CQCO=CRCB
- Substituting the known lengths:
yCO=x2x=12
- This implies:
CO=2y(Equation 1)
6. Use the Diagonal Bisecting Property:
- Since diagonals of a parallelogram bisect each other:
AO=OC
- Let OC=z, then AC=AO+OC=z+z=2z.
7. Relate AC and CQ:
- From Equation 1, we have OC=2y, thus:
AC=2(2y)=4y
- Therefore, we can express CQ in terms of AC:
CQ=14AC
8. Conclusion:
- The distance CQ is equal to one-fourth of the length of diagonal AC:
CQ=14AC
Final Answer:
The distance CQ will be equal to 14AC.
- Let A,B,C,D be the vertices of the parallelogram ABCD.
- P is the midpoint of DC.
- R is the midpoint of BC.
- Draw diagonal AC in the parallelogram.
- Join points P and R to form line PR.
- This line intersects diagonal AC at point Q.
- In triangle CQR and triangle COB (where O is the midpoint of diagonal AC):
- CQ is a side in triangle CQR.
- CR is half of CB since R is the midpoint of BC.
- Let CB=2x, then CR=x and CQ=y.
- By the properties of similar triangles:
CQCO=CRCB
- Substituting the known lengths:
yCO=x2x=12
- This implies:
CO=2y(Equation 1)
- Since diagonals of a parallelogram bisect each other:
AO=OC
- Let OC=z, then AC=AO+OC=z+z=2z.
- From Equation 1, we have OC=2y, thus:
AC=2(2y)=4y
- Therefore, we can express CQ in terms of AC:
CQ=14AC
- The distance CQ is equal to one-fourth of the length of diagonal AC:
CQ=14AC
The distance CQ will be equal to 14AC.
Similar Questions
Knowledge Check
In parallelogram ABCD,if P, Q are mid-points of BC and CD respectively, then ¯¯¯¯¯¯AP+¯¯¯¯¯¯AQ=
A32(¯¯¯¯¯¯AC)B54(¯¯¯¯¯¯AC)C(¯¯¯¯¯¯AC)D2(¯¯¯¯¯¯AC)ABCD is a parallelogram. P and Q are mid points of BC & CD. Find the area of ΔAPQ if area of ΔABC is 12.
AtrapeziumBparallelogramCsquareDnone of theseABCD a parallelogram, and A1andB1 are the midpoints of sides BC and CD, respectively. If −→aA1 +−−→AB1=λ−−→AC, then λ is equal to
A12B1C32D2
In a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionABCD is a parallelogram If M and N are the midpoints of BC and DC respectively,If ¯¯¯¯¯¯¯AM+¯¯¯¯¯¯AN=λ(¯¯¯¯¯¯AC) then value of λ
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
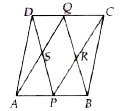
(i) APCQ is a parallelogram.
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

DPBQ is a parallelogram
View SolutionAssertion : In ΔABC,EandF are the midpoints of AC and AB respectively. The altitude AP at BC intersects FE at Q. Then, AQ = QP.
Reason : Q is the midpoint of AP.
View Solution