A syringe has a capacity of 5 ml. Its capacity in cm3 and m3 is respectively are
5×10−6m3,5cm3
5cm3,5×10−6m3
5×10−3m3,5cm3
5cm3,5×10−3m3
To solve the problem of converting the capacity of a syringe from milliliters (ml) to cubic centimeters (cm³) and cubic meters (m³), we can follow these steps:
1. Understand the Conversion from ml to cm³:
- We know that 1 milliliter (ml) is equivalent to 1 cubic centimeter (cm³).
- Therefore, if the syringe has a capacity of 5 ml, it directly translates to 5 cm³.
Calculation:
5ml=5cm3
2. Convert ml to m³:
- We need to convert milliliters to cubic meters.
- We know that 1 liter (L) is equal to 1000 ml, and 1 cubic meter (m³) is equal to 1000 liters.
- Thus, 1 m³ = 1,000,000 ml (since 1 m³ = 1000 L and 1 L = 1000 ml).
- Therefore, to convert ml to m³, we can use the conversion factor:
1ml=1×10−6m3
Calculation:
5ml=5×10−6m3
3. Final Answer:
- The capacity of the syringe in cm³ is 5 cm³.
- The capacity of the syringe in m³ is 5×10−6 m³.
Summary:
- The capacity of the syringe in cm³ is 5 cm³.
- The capacity of the syringe in m³ is 5×10−6 m³.
---
- We know that 1 milliliter (ml) is equivalent to 1 cubic centimeter (cm³).
- Therefore, if the syringe has a capacity of 5 ml, it directly translates to 5 cm³.
Calculation:
5ml=5cm3
- We need to convert milliliters to cubic meters.
- We know that 1 liter (L) is equal to 1000 ml, and 1 cubic meter (m³) is equal to 1000 liters.
- Thus, 1 m³ = 1,000,000 ml (since 1 m³ = 1000 L and 1 L = 1000 ml).
- Therefore, to convert ml to m³, we can use the conversion factor:
1ml=1×10−6m3
5ml=5×10−6m3
- The capacity of the syringe in cm³ is 5 cm³.
- The capacity of the syringe in m³ is 5×10−6 m³.
- The capacity of the syringe in cm³ is 5 cm³.
- The capacity of the syringe in m³ is 5×10−6 m³.
Topper's Solved these Questions
- MEASUREMENT BOOK - BEIITIANSCHAPTER - MEASUREMENT EXERCISE - IIT JEE WORKSHEET ( SINGLE CORRECT ANSWER TYPE)
7 Videos
- MEASUREMENT BOOK - BEIITIANSCHAPTER - MEASUREMENT EXERCISE - IIT JEE WORKSHEET ( SINGLE CORRECT ANSWER TYPE) FILL IN THE BLANKS.
1 Videos
- MEASUREMENT BOOK - BEIITIANSCHAPTER - MEASUREMENT EXERCISE - SUMMATIVE WORKSHEET
10 Videos
- MAGNETISMBOOK - BEIITIANSCHAPTER - MAGNETISMEXERCISE - IIT JEE Worksheet (Matrix Matching)
4 Videos
- MOTION & FORCEBOOK - BEIITIANSCHAPTER - MOTION & FORCEEXERCISE - IIT JEE WORKSHEET (II. MULTIPLE CORRECT ANSWER TYPE)
2 Videos
Similar Questions
Knowledge Check
The capacity and the energy stored in a parallel plate condenser with air between its plates are respectively C0 and W0. If the air is replaced by glass (dielectric constant =5) between the plates, the capacity of the plates and the energy stored in it will respectively be
A5C0,5W0B5C0,W05CC05,5W0DC05,W05In the circuit shown in figure, each capacitor has a capacity of 3μF. The equivalent capacity between A and B is
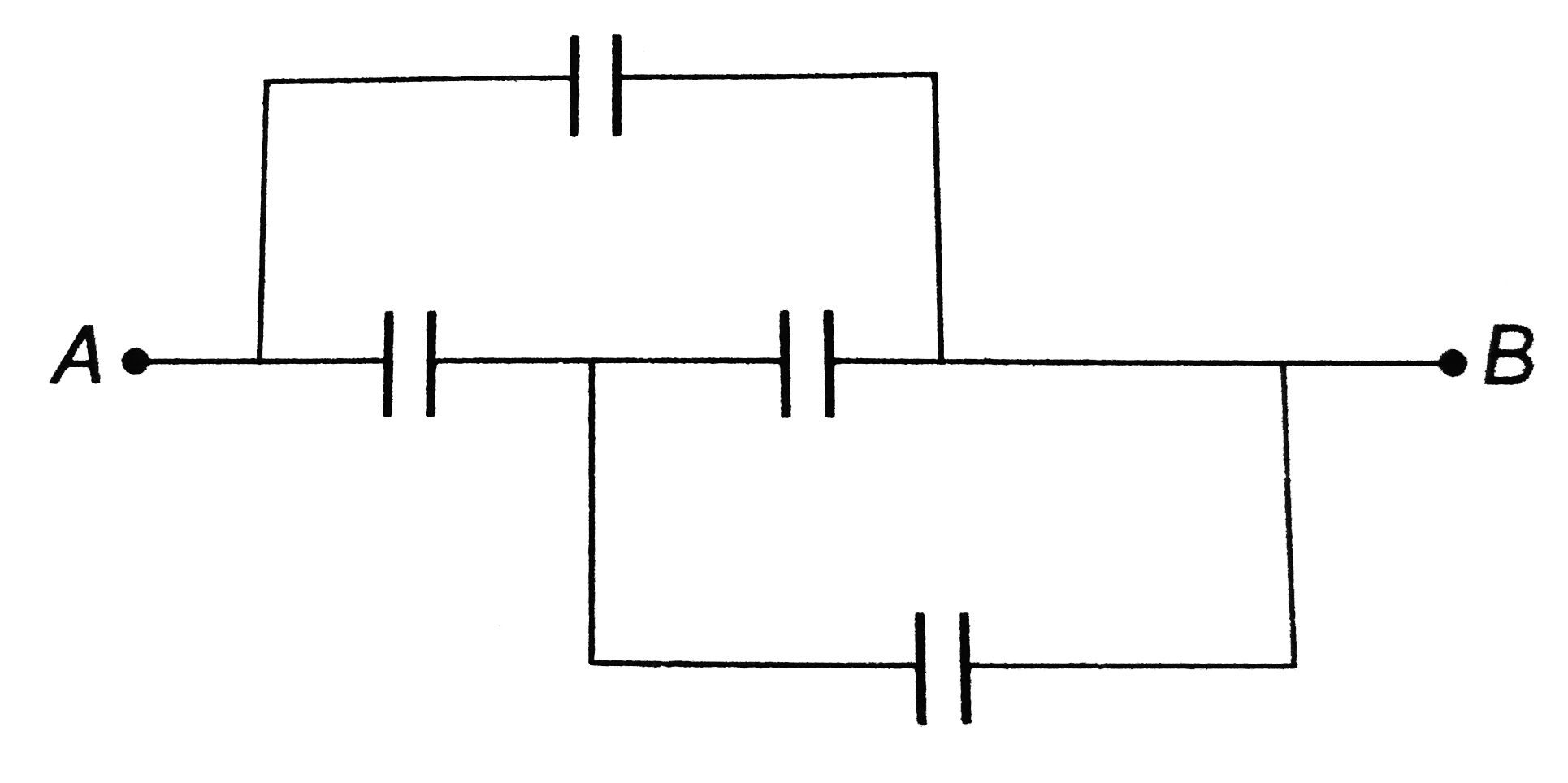 A36μFB3μFC6μFD5μF
A36μFB3μFC6μFD5μFConsider two conductors. One of them has a capacity of 2 units and the capacity of the other is unknown. They are charged until their potential are 4 and 5 units respectively. The two conductors are now connected by a wire when their common potential is found to be 4.6 units. Then the unknown capacity has the value (in the same units as above)
A6B5C4D3
A cylindrical tank has a capacity of 3080 cm3 .If its depth is 20 cm ,find its diameter
View Solution.A cylindrical tank has a capacity of 3080 cm3 and diameter of its base is 28 cm. Find its depth.
View SolutionA bucket is of height 25 cm. Its top and bottom radii are 20 cm and 10 cm respectively. Its capacity in litres is
View SolutionA body executing S.H.M. has its velocity 10cm/s and 7cm/s when its displacement from the mean positions are 3cm and 4cm respectively. Calculate the length of the path.
View SolutionThis section contains Assertion and Reason type questions. Each question has choices (1),(2), (3) and (4), out of which only one is correct.
Assertion (A) When a metallic plate is partially inserted between the plates of a capacity, its capacity increases.
Reason (R) If conductivity of conducting plate is more, increase in capacity will be more
View Solution
