If are masses of four bodies 0.3 g, 0.3 kg, g and 3000 g respectively. The above, in increasing order of masses, are as follows.
To solve the problem of arranging the masses m1,m2,m3, and m4 in increasing order, we need to convert all masses into the same unit for easy comparison. Let's follow these steps:
Step 1: Convert all masses to grams
The given masses are:
- m1=0.3g
- m2=0.3kg
- m3=0.3×10−6g
- m4=3000g
Convert m2 to grams:
m2=0.3kg×1000g/kg=300g
Convert m3 to grams:
m3=0.3×10−6g=0.3106g=0.0000003g
Now we have:
- m1=0.3g
- m2=300g
- m3=0.0000003g
- m4=3000g
Step 2: List the masses for comparison
Now we can list the masses:
- m1=0.3g
- m2=300g
- m3=0.0000003g
- m4=3000g
Step 3: Arrange the masses in increasing order
To arrange these masses in increasing order, we compare their values:
1. m3=0.0000003g (smallest)
2. m1=0.3g
3. m2=300g
4. m4=3000g (largest)
Thus, the increasing order of masses is:
m3<m1<m2<m4
Final Answer
The increasing order of the masses is:
m3,m1,m2,m4
---
The given masses are:
- m1=0.3g
- m2=0.3kg
- m3=0.3×10−6g
- m4=3000g
m2=0.3kg×1000g/kg=300g
m3=0.3×10−6g=0.3106g=0.0000003g
- m1=0.3g
- m2=300g
- m3=0.0000003g
- m4=3000g
Now we can list the masses:
- m1=0.3g
- m2=300g
- m3=0.0000003g
- m4=3000g
To arrange these masses in increasing order, we compare their values:
1. m3=0.0000003g (smallest)
2. m1=0.3g
3. m2=300g
4. m4=3000g (largest)
m3<m1<m2<m4
The increasing order of the masses is:
m3,m1,m2,m4
Topper's Solved these Questions
- MEASUREMENT Book:BEIITIANSChapter:MEASUREMENT Exercise:IIT JEE WORKSHEET ( SINGLE CORRECT ANSWER TYPE)
Explore 7 Videos
- MEASUREMENT Book:BEIITIANSChapter:MEASUREMENT Exercise:IIT JEE WORKSHEET ( SINGLE CORRECT ANSWER TYPE) FILL IN THE BLANKS.
Explore 1 Video
- MEASUREMENT Book:BEIITIANSChapter:MEASUREMENT Exercise:SUMMATIVE WORKSHEET
Explore 10 Videos
- MAGNETISMBook:BEIITIANSChapter:MAGNETISMExercise:IIT JEE Worksheet (Matrix Matching)
Explore 4 Videos
- MOTION & FORCEBook:BEIITIANSChapter:MOTION & FORCEExercise:IIT JEE WORKSHEET (II. MULTIPLE CORRECT ANSWER TYPE)
Explore 2 Videos
Similar Questions
If m1,m2,m3 and m4 are masses of four bodies 0.3 kg, 0.3 mg, 0.3×10−6g nad 3000 g respectively. The above in increasing order of masses are as sollows
View SolutionAt 800 K in a sealed vessel for the equilibrium N2(g)+O2(g)⇔2NO(g), the equilibrium concentrations of N2(g),O2(g) and NO(g) are respectively 0.36×10−3M,4.41×10−3Mand1.4×10−3M. Calculate the value of Kc for the reaction NO(g)⇔1/2N2(g)+1/2O2(g)at800Kis:
View Solution
Knowledge Check
Two bodies of mass 2 kg and 5 kg have position (1 m, 2 m, 1 m) and (3 m, 2 m, -1 m) respectively. The position vector of centre of mass is
A(177ˆi+2ˆj−37ˆk)mB(17ˆi+14ˆj−3ˆk)mC(2ˆi+177ˆj−37ˆk)mD(14ˆi+17ˆj−3ˆk)mThree blocks I,II, & III having mass of 1.6kg, 1.6kg and 3.2kg repectively are connected as shown in the figure. The linear mass density of the wire AB,CD and DE are 10g/m,8g/m and 10g/m respectively. The speed of a transverse wave pulse produced in AB,CD and DE are : (g=10m/sec2)
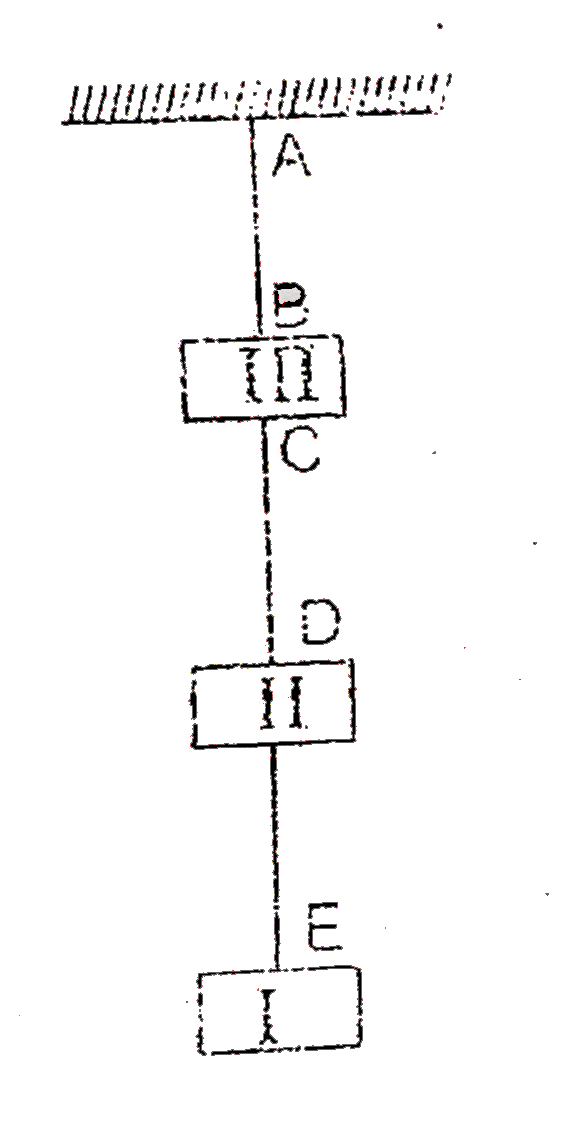 A80m/s,20√10m/s,40m/sB20√10m/s,40m/s,80m/sC20√10m/s in allD80m/s in all
A80m/s,20√10m/s,40m/sB20√10m/s,40m/s,80m/sC20√10m/s in allD80m/s in allThe centres of three spherical masses of 1 kg, 2 kg and 3 kg have co-orinates (4,0) m,(0,3)m and (-2,5)m respectively. What is the position vector of its centre of mass is terms of its x and y co-ordinates?
A→Rcm=2ˆi+3ˆjB→RcM=13ˆi+52ˆjCveRcm=≡−13ˆi+3.5ˆjD→rcm=23ˆi−53ˆj
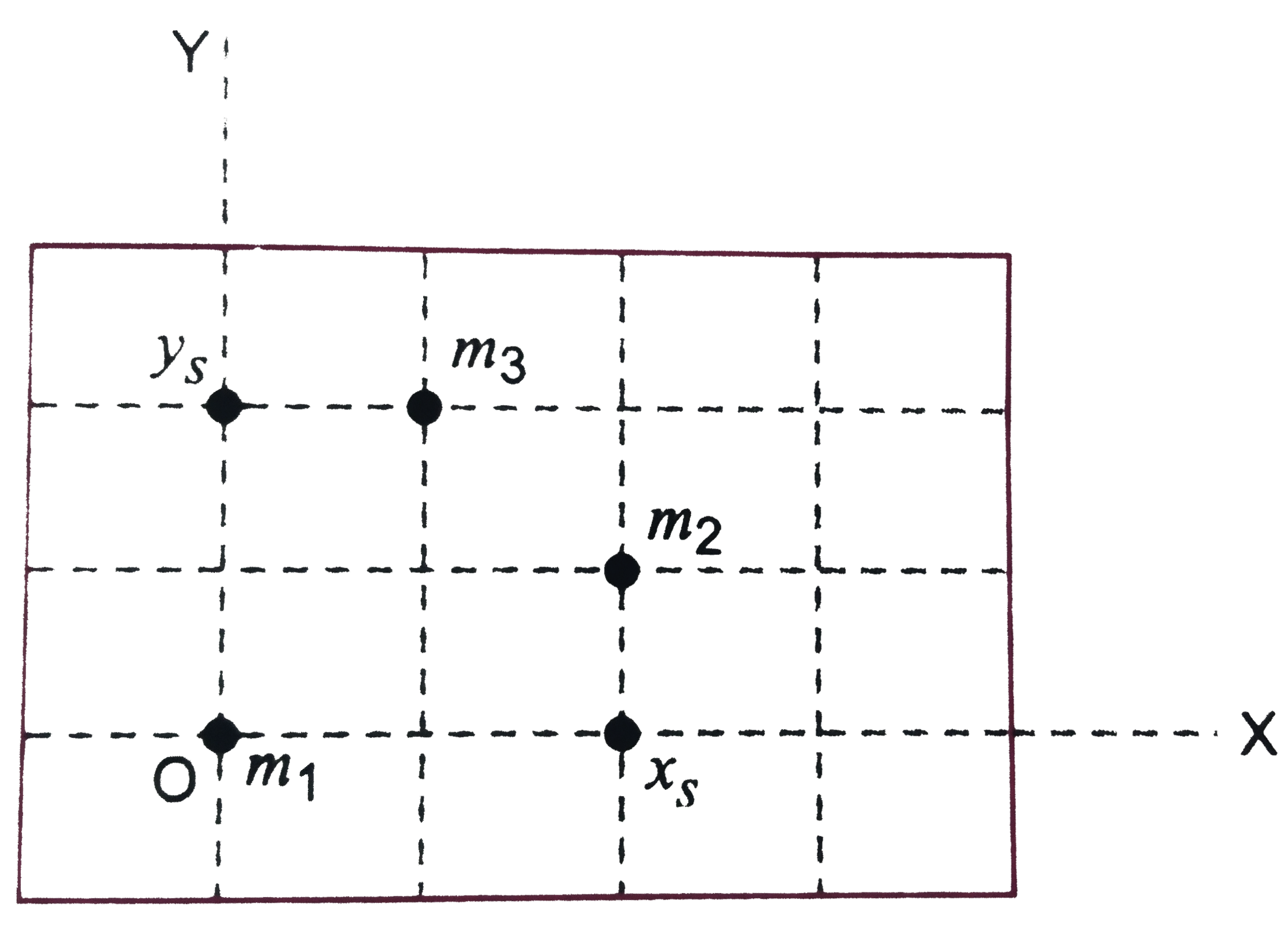
Fig. shown a three particle system with masses m1=3.0kg,m2=4.0kg and m3=8.0kg. The scales on the axes are set by xs=2.0m and ys=2.0m. What are the co-ordinates of centre if mass ? If m3 is gradually increased, does the centre of mass of the system shift towards or away from that particle or does it remain stationary ?
View SolutionA mass of 1 kg is placed at (1m, 2m, 0). Another mass of 2 kg is placed at (3m, 3m, 0). Find the moment of inertial of both the masses about z-axis
View Solution10 kg m−3 =____g cm−3
View SolutionThe mass of a body is 20.0 g and its volume is 10.0cm3. If possible maximum errors in the measurement of mass of body and volume of body are 0.001 g and 0.01cm3 respectively, then the maximum error in the value of density is
View SolutionThe measured mass and volume of a body are 22.42g and 4.cm3, respectively, with possible errors of 0.01g and 0.1cm3. The maximum error in density is
View Solution
