When 234 is divided by 9 , the remainder will be?
a) 7
b) 8
c) 5
d) 6
The correct Answer is:a
To find the remainder when 234 is divided by 9, we can use the concept of modular arithmetic and properties of exponents. Here’s a step-by-step solution:
Step 1: Identify the problem
We need to find 234mod9.
Step 2: Use properties of exponents
Instead of calculating 234 directly, we can look for a pattern in the powers of 2 modulo 9.
Step 3: Calculate the first few powers of 2 modulo 9
- 21=2
- 22=4
- 23=8
- 24=16≡7mod9 (since 16−9=7)
- 25=32≡5mod9 (since 32−27=5)
- 26=64≡1mod9 (since 64−63=1)
Step 4: Identify the cycle
From the calculations, we see that 26≡1mod9. This means every sixth power of 2 will repeat the cycle:
- 21≡2
- 22≡4
- 23≡8
- 24≡7
- 25≡5
- 26≡1
Step 5: Reduce the exponent modulo 6
Since 26≡1mod9, we can reduce 34 modulo 6:
34÷6=5(with a remainder of 4)
Thus, 34mod6=4.
Step 6: Find 24mod9
From our earlier calculations:
24≡7mod9
Conclusion
Therefore, the remainder when 234 is divided by 9 is 7.
Final Answer
The remainder is 7.
---
We need to find 234mod9.
Instead of calculating 234 directly, we can look for a pattern in the powers of 2 modulo 9.
- 21=2
- 22=4
- 23=8
- 24=16≡7mod9 (since 16−9=7)
- 25=32≡5mod9 (since 32−27=5)
- 26=64≡1mod9 (since 64−63=1)
From the calculations, we see that 26≡1mod9. This means every sixth power of 2 will repeat the cycle:
- 21≡2
- 22≡4
- 23≡8
- 24≡7
- 25≡5
- 26≡1
Since 26≡1mod9, we can reduce 34 modulo 6:
34÷6=5(with a remainder of 4)
Thus, 34mod6=4.
From our earlier calculations:
24≡7mod9
Therefore, the remainder when 234 is divided by 9 is 7.
The remainder is 7.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
When 233 is divided by 10, the remainder will be
A2B3C4D8 - Question 2 - Select One
When (98+1) is divided by 8, the remainder will be?
Aa)3Bb)2Cc)1Dd)4 - Question 3 - Select One
When 231 is divided by 5 the remainder is
A4B3C2D1
When 90707 is divided by 9, the remainder is
View SolutionWhen
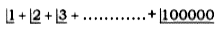 is divided by 8 then the remainder will be? View Solution
is divided by 8 then the remainder will be? View SolutionWhen
 is divided by 12 then the remainder will be? View Solution
is divided by 12 then the remainder will be? View SolutionWhen (719+2) is divided by 6 then remainder will be?
View SolutionIf the difference of remainders, obtained on dividing 26679 by 39 and 29405 by 34, is divided by 18, then the remainder will be
View Solution

