When 5507 is divided by 500, the remain- der will be?
125
1
121
4
The correct Answer is:a
To find the remainder when 5507 is divided by 500, we can simplify the problem step by step.
Step 1: Factor 500
First, we can factor 500:
500=53×22=125×4
Step 2: Rewrite the expression
We want to find 5507mod500. We can express 5507 in terms of its factors:
5507=5504×53
Step 3: Simplify using the factor of 500
Since 5504 contains 53, we can rewrite it as:
5507=5504×125
Now, we can express 5504 in terms of 500:
5507=125×5504
Step 4: Calculate 5504mod4
Next, we need to find 5504mod4. Since 5≡1mod4:
5504≡1504≡1mod4
Step 5: Calculate 5507mod125
Now, we calculate 5507mod125:
5507≡0mod125
because 507>3.
Step 6: Use the Chinese Remainder Theorem
Now we have two congruences:
1. 5507≡0mod125
2. 5507≡1mod4
Let x be the remainder we are looking for. We can set up the system:
x≡0mod125
x≡1mod4
Step 7: Solve the system of congruences
From the first congruence, we can express x as:
x=125kfor some integer k
Substituting into the second congruence:
125k≡1mod4
Calculating 125mod4:
125≡1mod4
Thus:
1k≡1mod4⟹k≡1mod4
So, we can write:
k=4m+1for some integer m
Substituting back:
x=125(4m+1)=500m+125
Step 8: Find the remainder
Thus, the remainder when x is divided by 500 is:
x≡125mod500
Final Answer
The remainder when 5507 is divided by 500 is 125.
First, we can factor 500:
500=53×22=125×4
We want to find 5507mod500. We can express 5507 in terms of its factors:
5507=5504×53
Since 5504 contains 53, we can rewrite it as:
5507=5504×125
Now, we can express 5504 in terms of 500:
5507=125×5504
Next, we need to find 5504mod4. Since 5≡1mod4:
5504≡1504≡1mod4
Now, we calculate 5507mod125:
5507≡0mod125
because 507>3.
Now we have two congruences:
1. 5507≡0mod125
2. 5507≡1mod4
x≡0mod125
x≡1mod4
From the first congruence, we can express x as:
x=125kfor some integer k
125k≡1mod4
Calculating 125mod4:
125≡1mod4
Thus:
1k≡1mod4⟹k≡1mod4
So, we can write:
k=4m+1for some integer m
Substituting back:
x=125(4m+1)=500m+125
Thus, the remainder when x is divided by 500 is:
x≡125mod500
The remainder when 5507 is divided by 500 is 125.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
When 799 is divided by 2400, the remain- der obtained is ?
A1B49C343D7 - Question 2 - Select One
When number 101+102+103+104+.............+1011 is divided by 6, the remain- der will be?
A4B2C5D1 - Question 3 - Select One
When 231 is divided by 5 the remainder is
A4B3C2D1
When (5)501 is divided by 126, the remainder is :
View SolutionWhen 321684 is divided by 5, the remainder is
View SolutionWhen 231 is divided by 5 the remainder is
View SolutionA number when divided by 5 leaves a remainder of 4, when the double (i.e., twice) of that number is divided by 5 the remainder will be :
View SolutionWhen
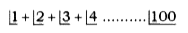 , is divided by 5, the remainder obtained is ?View Solution
, is divided by 5, the remainder obtained is ?View Solution

