When 777777 ............ 363 times, is divided by 11, the remainder obtained is?
10
7
3
8
The correct Answer is:b
To solve the problem of finding the remainder when the number formed by repeating 777 a total of 363 times is divided by 11, we can follow these steps:
1. Understanding the Number:
The number we are dealing with is 777 repeated 363 times. We can denote this number as N=777777... (363 times).
2. Finding the Remainder of 777:
First, we need to find the remainder when 777 is divided by 11.
777÷11=70(whole part)
70×11=770
Remainder=777−770=7
So, 777≡7mod11.
3. Finding the Remainder of the Repeated Number:
Since N consists of 363 occurrences of 777, we can express N as:
N=777×(103×362+103×361+...+100)
The sum inside the parentheses is a geometric series with 363 terms, where the first term a=1 and the common ratio r=103.
4. Calculating the Sum of the Geometric Series:
The sum S of the geometric series can be calculated using the formula:
S=a(rn−1)r−1
Here, n=363, a=1, and r=103:
S=1×((103)363−1)103−1=(101089−1)999
5. Finding the Remainder of S Modulo 11:
We need to find Smod11. By Fermat's Little Theorem, since 10≡−1mod11:
101089≡(−1)1089≡−1mod11
Thus,
101089−1≡−1−1≡−2mod11
Now, we need to find 999mod11:
999÷11=90(whole part)
90×11=990
Remainder=999−990=9
So, 999≡9mod11.
6. Final Calculation:
Now we can calculate Smod11:
S≡−29mod11
To find −29mod11, we need the multiplicative inverse of 9 modulo 11. The inverse of 9 can be found by checking:
9×5≡45≡1mod11
Therefore, the inverse is 5. Now we can compute:
S≡−2×5≡−10≡1mod11
7. Finding the Final Remainder:
Now, we multiply this result by the remainder of 777:
N≡7×1≡7mod11
Conclusion:
The remainder when the number formed by repeating 777 a total of 363 times is divided by 11 is 7.
The number we are dealing with is 777 repeated 363 times. We can denote this number as N=777777... (363 times).
First, we need to find the remainder when 777 is divided by 11.
777÷11=70(whole part)
70×11=770
Remainder=777−770=7
So, 777≡7mod11.
Since N consists of 363 occurrences of 777, we can express N as:
N=777×(103×362+103×361+...+100)
The sum inside the parentheses is a geometric series with 363 terms, where the first term a=1 and the common ratio r=103.
The sum S of the geometric series can be calculated using the formula:
S=a(rn−1)r−1
Here, n=363, a=1, and r=103:
S=1×((103)363−1)103−1=(101089−1)999
We need to find Smod11. By Fermat's Little Theorem, since 10≡−1mod11:
101089≡(−1)1089≡−1mod11
Thus,
101089−1≡−1−1≡−2mod11
Now, we need to find 999mod11:
999÷11=90(whole part)
90×11=990
Remainder=999−990=9
So, 999≡9mod11.
Now we can calculate Smod11:
S≡−29mod11
To find −29mod11, we need the multiplicative inverse of 9 modulo 11. The inverse of 9 can be found by checking:
9×5≡45≡1mod11
Therefore, the inverse is 5. Now we can compute:
S≡−2×5≡−10≡1mod11
Now, we multiply this result by the remainder of 777:
N≡7×1≡7mod11
The remainder when the number formed by repeating 777 a total of 363 times is divided by 11 is 7.
Topper's Solved these Questions
Similar Questions
Knowledge Check
When
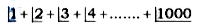 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7777777 .......... 129 times is divided by 37, the remainder obtained is ?
A0B37C1D36When
 is divided by 10, the remaindeer obtained is ? A3B1C2D9
is divided by 10, the remaindeer obtained is ? A3B1C2D9
When 666666 ........... 134 times, is divided by 13, the remainder obtained is?
View SolutionWhen 221 is divided by 9, the remainder obtained is ?
View SolutionWhen 1177 is divided by 7, the remainder obtained is ?
View SolutionWhen 4177 is divided by 17, the remainder obtained is ?
View SolutionWhen 355 is divided by 82, the remainder obtained is ?
View Solution

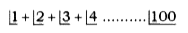 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?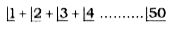 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?