When 4177 is divided by 17, the remainder obtained is ?
2
1
6
4
The correct Answer is:c
To find the remainder when 4177 is divided by 17, we can use Fermat's Little Theorem, which states that if p is a prime number and a is an integer not divisible by p, then:
ap−1≡1modp
In this case, p=17 and a=41.
Step 1: Reduce 41 modulo 17
First, we need to find 41mod17:
41÷17=2(quotient)
41−(17×2)=41−34=7
So, 41≡7mod17.
Step 2: Rewrite the expression
Now we can rewrite 4177 as:
4177≡777mod17
Step 3: Apply Fermat's Little Theorem
According to Fermat's Little Theorem, since 7 is not divisible by 17:
716≡1mod17
Step 4: Reduce the exponent modulo 16
Next, we need to reduce 77 modulo 16:
77÷16=4(quotient)
77−(16×4)=77−64=13
So, 77≡13mod16.
Step 5: Calculate 713mod17
Now we need to compute 713mod17. We can do this by calculating powers of 7:
71≡7mod17
72≡49mod17≡15mod17
73≡7×15=105mod17≡3mod17
74≡7×3=21mod17≡4mod17
75≡7×4=28mod17≡11mod17
76≡7×11=77mod17≡13mod17
77≡7×13=91mod17≡6mod17
78≡7×6=42mod17≡8mod17
79≡7×8=56mod17≡5mod17
710≡7×5=35mod17≡1mod17
711≡7×1=7mod17
712≡7×7=49mod17≡15mod17
713≡7×15=105mod17≡3mod17
Step 6: Conclusion
Thus, the remainder when 4177 is divided by 17 is:
3
First, we need to find 41mod17:
41−(17×2)=41−34=7
Now we can rewrite 4177 as:
According to Fermat's Little Theorem, since 7 is not divisible by 17:
Next, we need to reduce 77 modulo 16:
77−(16×4)=77−64=13
Now we need to compute 713mod17. We can do this by calculating powers of 7:
72≡49mod17≡15mod17
73≡7×15=105mod17≡3mod17
74≡7×3=21mod17≡4mod17
75≡7×4=28mod17≡11mod17
76≡7×11=77mod17≡13mod17
77≡7×13=91mod17≡6mod17
78≡7×6=42mod17≡8mod17
79≡7×8=56mod17≡5mod17
710≡7×5=35mod17≡1mod17
711≡7×1=7mod17
712≡7×7=49mod17≡15mod17
713≡7×15=105mod17≡3mod17
Thus, the remainder when 4177 is divided by 17 is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
When 1177 is divided by 7, the remainder obtained is ?
A2B3C5D1 - Question 2 - Select One
When 54124 is divided by 17, the remainder obtained is ?
A4B5C3D15 - Question 3 - Select One
When
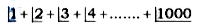 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7
When 52450 is divided by 126, the remainder obtained is ?
View SolutionWhen
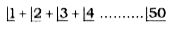 , is divided by 12, the remainder obtained is ?View Solution
, is divided by 12, the remainder obtained is ?View SolutionWhen
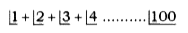 , is divided by 5, the remainder obtained is ?View Solution
, is divided by 5, the remainder obtained is ?View SolutionWhen 740 is divided by 400, the remainder obtained is ?
View SolutionWhen (35)37 is divided by 9 the remainder obtained is ?
View Solution


 is divided by 10, the remaindeer obtained is ?
is divided by 10, the remaindeer obtained is ?