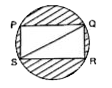
In the figure given figure, PQRS is a square inscribed in a circle of radius 4 cm. PQ is produced till point Y. From Y a tangent in drawn to the circle at point R (QR=QY). What is the length (in cm) of SY?
a)4√10
b)2√10
c)6√10
d)3√5
Step by step video & image solution for In the figure given figure, PQRS is a square inscribed in a circle of radius 4 cm. PQ is produced till point Y. From Y a tangent in drawn to the circle at point R (QR=QY). What is the length (in cm) of SY? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure given figure, PQRS is a square inscribed in a circle of radius 4 cm. PQ is produced till point Y. From Y a tangent in drawn to the circle at point R (QR=QY). What is the length (in cm) of SY?
 A4√10B2√10C6√10D3√5
A4√10B2√10C6√10D3√5A circle with radius r has a chord PQ whose length is 2a. The tangents drawn at points PandQ to the circle meet at T, what is the length of TP?
Aar√r2−a2B2ar√r2−a2Cr2+a2√r2−a2Darr−aTriangle PQR is inscribed in the circle whose radius is 14 cm. If PQ is the diameter of the circle and PR = 10 cm, then what is the area of the triangle PQR ?
A196B30√19C40√17D35√21
In the given figure, PQRS is a square whose side is 8 cm. PQS and QPR are two quadrants. A circle is placed touching both the Quadrants and the square as shown in the figure. What is the area (in cm2) of the circle?
View SolutionA point P is at a distance of 29cm from the centre of a circle of radius 20cm. Find the length of the tangent drawn from P to the circle.
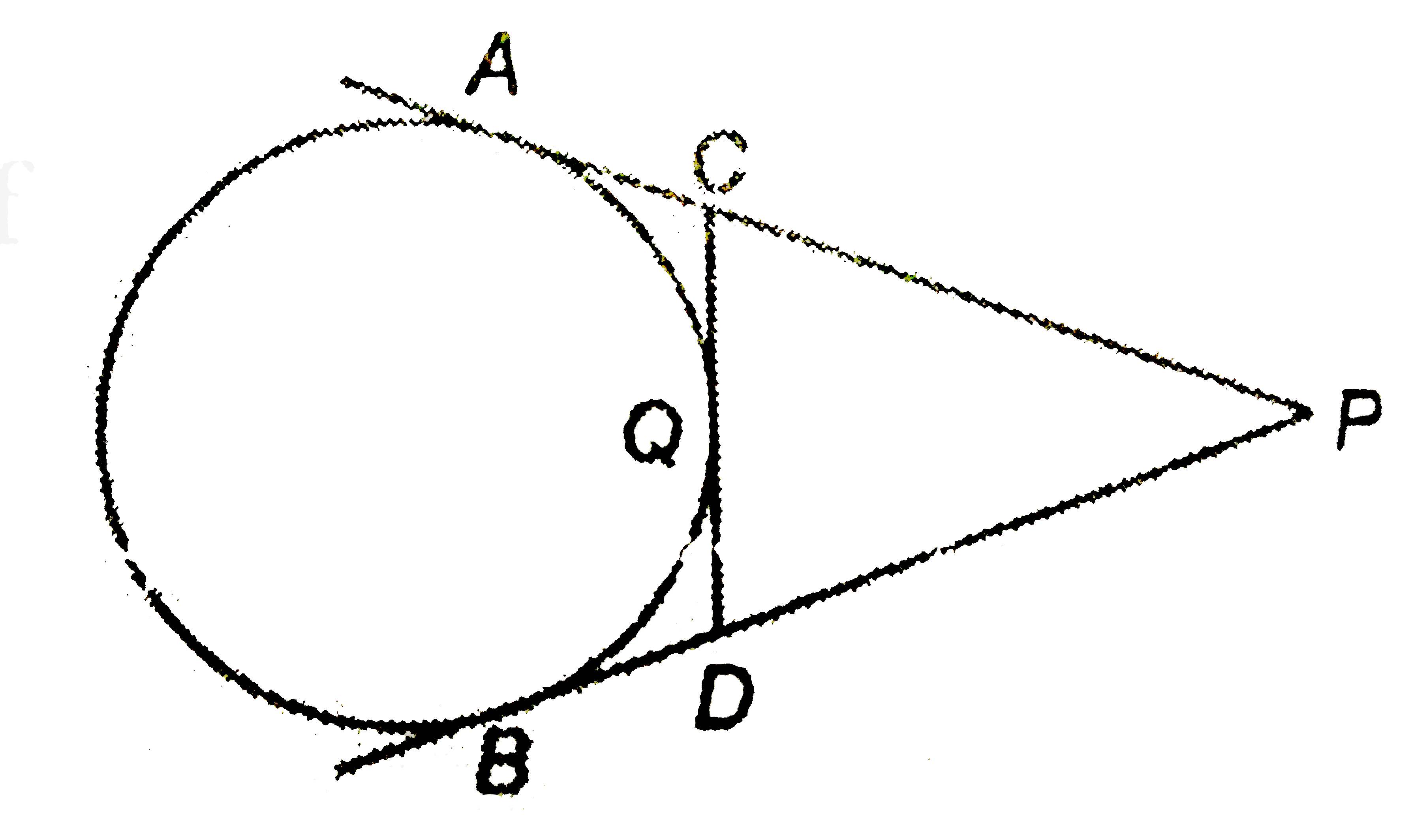
View SolutionIn the given figure PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB=10cm and CQ=2cm. What is the length of PC?
View SolutionDraw a circle of radius 3 cm. From a point 5 cm from the centre of the circle, draw two tangents to the circle. Measure the length of each tangent.
View SolutionThe length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is
View Solution