Two circles touch each other at point X. Two common tangents of the circles meet at point P and none of the tangents passes through X. These tangents touch the larger circle at points B and C. If the radius of the larger circle is 15 cm and CP = 20 cm, then what is the radius (in cm) of the smaller circle?
3.5
3.75
4.25
4.45
To find the radius of the smaller circle, we can follow these steps:
Step 1: Understand the Problem
We have two circles that touch each other at point X. The larger circle has a radius of 15 cm, and the distance from point P (where the tangents meet) to point C (where the tangent touches the larger circle) is 20 cm. We need to find the radius of the smaller circle.
Step 2: Draw the Diagram
Draw two circles, one larger and one smaller, touching each other at point X. Mark the center of the larger circle as O and the center of the smaller circle as O'. Draw the common tangents that touch the larger circle at points B and C, and meet at point P.
Step 3: Identify Known Values
- Radius of the larger circle (OB) = 15 cm
- Length of CP = 20 cm
- Length of BP = 20 cm (since BP = CP)
Step 4: Apply the Pythagorean Theorem
In triangle OBP, we apply the Pythagorean theorem to find OP:
OP=√BP2+OB2
Substituting the known values:
OP=√202+152=√400+225=√625=25 cm
Step 5: Relate OP and O'P
We know that:
O′P=OP−OO′
Where OO′=OB+O′B (the radius of the larger circle plus the radius of the smaller circle). Let the radius of the smaller circle be r:
OO′=15+r
Thus,
O′P=25−(15+r)=10−r
Step 6: Set Up Similar Triangles
Triangles OBP and O'DP are similar because they share angle BOP and both have a right angle at B and D respectively. Therefore, we can set up the ratio of their corresponding sides:
BPDP=OPO′P=OBO′D
Where DP=O′P and O′D=r.
Step 7: Substitute Known Values
From the similarity of triangles:
20DP=2510−r=15r
Step 8: Cross Multiply
From the equation:
2510−r=15r
Cross multiplying gives:
25r=15(10−r)
Expanding this:
25r=150−15r
Step 9: Solve for r
Combine like terms:
25r+15r=150
40r=150
Divide by 40:
r=15040=3.75 cm
Conclusion
The radius of the smaller circle is 3.75 cm.
---
We have two circles that touch each other at point X. The larger circle has a radius of 15 cm, and the distance from point P (where the tangents meet) to point C (where the tangent touches the larger circle) is 20 cm. We need to find the radius of the smaller circle.
Draw two circles, one larger and one smaller, touching each other at point X. Mark the center of the larger circle as O and the center of the smaller circle as O'. Draw the common tangents that touch the larger circle at points B and C, and meet at point P.
- Radius of the larger circle (OB) = 15 cm
- Length of CP = 20 cm
- Length of BP = 20 cm (since BP = CP)
In triangle OBP, we apply the Pythagorean theorem to find OP:
OP=√BP2+OB2
Substituting the known values:
OP=√202+152=√400+225=√625=25 cm
We know that:
O′P=OP−OO′
Where OO′=OB+O′B (the radius of the larger circle plus the radius of the smaller circle). Let the radius of the smaller circle be r:
OO′=15+r
Thus,
O′P=25−(15+r)=10−r
Triangles OBP and O'DP are similar because they share angle BOP and both have a right angle at B and D respectively. Therefore, we can set up the ratio of their corresponding sides:
BPDP=OPO′P=OBO′D
Where DP=O′P and O′D=r.
From the similarity of triangles:
20DP=2510−r=15r
From the equation:
2510−r=15r
Cross multiplying gives:
25r=15(10−r)
Expanding this:
25r=150−15r
Combine like terms:
25r+15r=150
40r=150
Divide by 40:
r=15040=3.75 cm
The radius of the smaller circle is 3.75 cm.
Topper's Solved these Questions
Similar Questions
In two concentric circles, a chord of length 8cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5cm then find the radius of the smaller circle.
View SolutionTwo circles touch each other at point X. A common tangent touch them at two distinet points Y and Z. If another tangent passing through X cut YZ at A and XA = 15 cm, then what is the value (in cm) of YZ?
View Solution
Knowledge Check
Two circles touch each other externally at a point P and a direct common tangent touches the circles at the points Q and R respectively. Then ∠QPR is
A45∘B180∘C90∘D60∘In the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
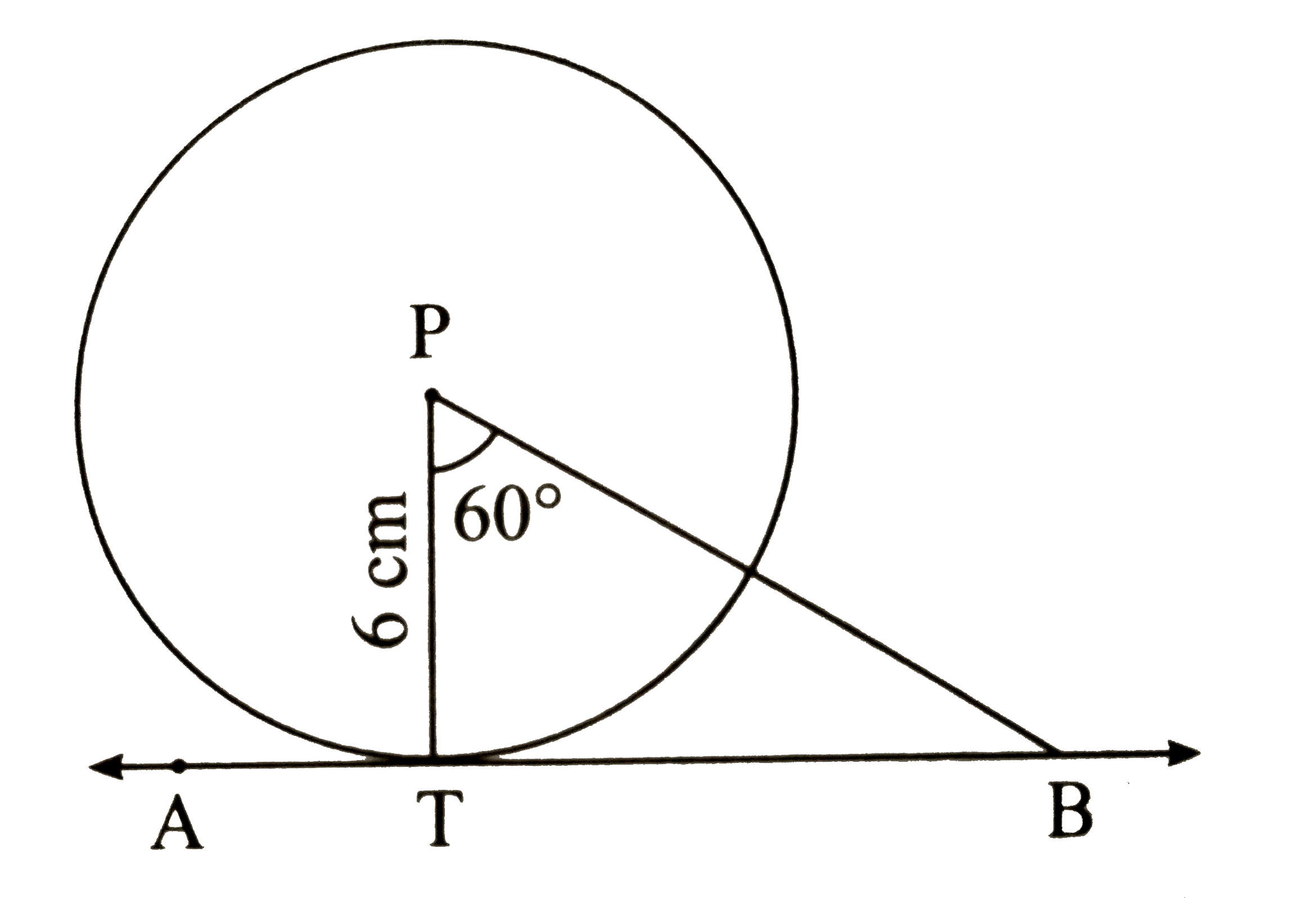 A5√5cmB10√5cmC(10−5√3)cmD(10−5√3)cm
A5√5cmB10√5cmC(10−5√3)cmD(10−5√3)cmTwo circles touch each other externally at point A and PQ is a direct tangent which touch circle at P and Q respectively then ∠PAQ = ?
A60∘B30∘C90∘D45∘
Two circles touch each other externally at point P. A common tangent AB is drawn touching the circles at A and B. Find ∠APB.
View SolutionIn Fig. 10.21, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q . (FIGURE)
View SolutionTwo circles touch each other externally. The distance between their centres is 8 cm. If the radius of one circle is 3 cm, then the radius of the other circle is:
दो वृत्त एक दूसरे को बाह्य रूप से स्पर्श करते हैं। उनके केंद्रों के बीच की दूरी 8 सेमी है। यदि एक वृत्त की त्रिज्या 3 सेमी है, तो दूसरे वृत्त की त्रिज्या है:
View SolutionTwo circles touch each other externally at point A and PQ is a direct tangent which touch circle at P and Q respectively then ∠PAQ = ?
View SolutionTwo circle touch each other externally at the point (0,k) and y-axis is the common tangent to these circles. Centres of these circle lie on the line
View Solution
