ABC is rt angled triangle ∠BAC=90∘and∠ACB=60∘. What is the ratio of the circum radius of the triagle to the side AB?
1:2
1:√3
2:√3
2:3
To find the ratio of the circumradius (R) of triangle ABC to the side AB, we can follow these steps:
Step 1: Identify the angles and sides of the triangle
Given:
- Triangle ABC is a right-angled triangle.
- Angle BAC = 90° (right angle)
- Angle ACB = 60°
From this, we can determine that:
- Angle ABC = 30° (since the sum of angles in a triangle is 180°).
Step 2: Use the properties of a right triangle
In a right triangle, the circumradius (R) can be calculated using the formula:
R=c2
where c is the length of the hypotenuse.
Step 3: Determine the sides of the triangle using trigonometric ratios
Let:
- AB = a (the side opposite angle ACB)
- AC = b (the side opposite angle ABC)
- BC = c (the hypotenuse)
Using the sine function for angle ACB (60°):
sin(60°)=ABBC
√32=ac
Thus,
a=c⋅√32
Step 4: Substitute the value of the hypotenuse in the circumradius formula
From the circumradius formula:
R=c2
Step 5: Find the ratio of circumradius to side AB
Now, we need to find the ratio RAB:
RAB=c2a
Substituting a from step 3:
RAB=c2c⋅√32
This simplifies to:
RAB=1√3
Final Result
Thus, the ratio of the circumradius of triangle ABC to the side AB is:
RAB=1√3
Given:
- Triangle ABC is a right-angled triangle.
- Angle BAC = 90° (right angle)
- Angle ACB = 60°
- Angle ABC = 30° (since the sum of angles in a triangle is 180°).
In a right triangle, the circumradius (R) can be calculated using the formula:
R=c2
where c is the length of the hypotenuse.
Let:
- AB = a (the side opposite angle ACB)
- AC = b (the side opposite angle ABC)
- BC = c (the hypotenuse)
sin(60°)=ABBC
√32=ac
Thus,
a=c⋅√32
From the circumradius formula:
R=c2
Now, we need to find the ratio RAB:
RAB=c2a
Substituting a from step 3:
RAB=c2c⋅√32
This simplifies to:
RAB=1√3
Thus, the ratio of the circumradius of triangle ABC to the side AB is:
RAB=1√3
Topper's Solved these Questions
Similar Questions
In the given figure, ABC is a right angled triangle. ∠ABC=90∘and∠ACB=60∘. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle?
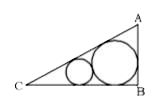
View SolutionIn a right angled triangle ABCABC=90∘,ACB=30∘ and AB=8cm. Find the length of the other sides of the triangle.
View Solution
Knowledge Check
ABCis a right angled triangle. ∠BAC=90∘ and ∠ACB=60∘. What is the ratio of the circum radius of the triangle to the side AB ?
A1:2B1:13C2:13D2:3In the given figure, ABC is a right angled triangle. ∠ABC=90∘and∠ACB=60∘. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle?
 A4B6C4.5D7.5
A4B6C4.5D7.5ABC is a right angled triangle right angled at Band∠A=60∘andAB=20cm , then the ratio of sides BC and CA is
A√3:1B1:√3C√3:√2D√3:2
In a ΔABC,∠A=90∘,∠B=30∘ find the ratio of sides .
View SolutionIn a triangle ABC, ∠ABC=90∘,∠ACB=30∘,AB=5cm. What is the length of AC?
View SolutionIn a triangle ABC, ∠B=2∠C=2∠A. What is the ratio of AC to AB ?
View SolutionIn the given figure, ABC is a right angled triangle. ∠ABC=900 and ∠ACB=600. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle?
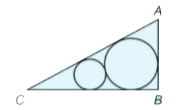
View SolutionI is the incentre of the triangle ABC. If ∠ABC=60∘ and ∠ACB=50∘ then ∠BIC is
View Solution
