ΔABC is a right triangle which is right angled at C. A circle is drawn taking AB as a diameter. AC is extended to point P. BP meet semicircle at D, then AB2 =
AC×AP+BD×BP
AC×BD+AP×BP
PD2−PC×CA
AC×AP+PD×DB
Step by step video & image solution for DeltaABC is a right triangle which is right angled at C. A circle is drawn taking AB as a diameter. AC is extended to point P. BP meet semicircle at D, then AB^(2) = by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
ΔABC is a right triangle , right angled at A and AD⊥BC . If AB= c and AC = b, then AD is equal to
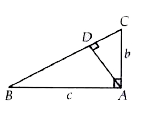 Abc√b2+c2Bbcb2+c2Cb2c√b2+c2DNone of these
Abc√b2+c2Bbcb2+c2Cb2c√b2+c2DNone of theseABC is a right angled triangle, right angled at C. If ∠A=60∘andAB=40 unit, then the length of AC is
A30 unitB20 unitC40 unitDNone of theseABC is a right angled triangle, right angled at C. If ∠A=60∘andAB=40 unit, then the length of AC is
A30 unitB20 unitC40 unitDNone of these
ΔABD is a right triangle, right-angled at A and AC⊥BD. Prove that AB2=BC×BD.
View SolutionIn Fig 12.58, ABC is a triangle right angled at A. Semicircles are drawn on AB and AC as diameters. Find the area of the shaded region.
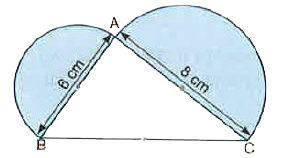
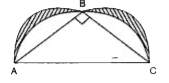
View SolutionIn the given figure, ABC is a right angled triangle with B as right angle. Three semicircles are drawn with AB, BC and AC as diameters. What is the area of the shaded portion, if the area of ΔABC is 12 square units ?
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View Solution

