Question

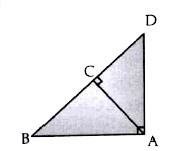
$\Delta ABD$ is a right triangle, right-angled at A and $AC\perp BD$.
Prove that $A{B}^2=BC\times BD$.

Explanation

To prove that $$A{B}^2=BC\times BD$$ in triangle $$\Delta ABD$$ where $$A$$ is the right angle and $$AC\perp BD$$, we will use the properties of similar triangles.

1. Identify the triangles: We have two triangles, \( \Delta ABC \) and \( \Delta ABD \). Note that \( A \) is the right angle in triangle \( ABD \).

2. Establish angles: Since \( AC \perp BD \), angle \( ACB \) is also a right angle. Therefore, we have:
\( \angle BAD = \angle ACB = 90^\circ \)

3. Identify common angles: Both triangles \( \Delta ABC \) and \( \Delta ABD \) share angle \( ABC \). Thus, we can say:
\( \angle ABC = \angle ABD \)

4. Use the angle sum property: Since the angles in a triangle sum up to \( 180^\circ \), we can find the third angles:
\( \angle BAC = \angle ADB \)

5. Establish similarity: By the AA (Angle-Angle) criterion for similarity, we conclude that:
\( \Delta ABC \sim \Delta ABD \)

6. Set up the proportionality: From the similarity of triangles, the sides are proportional:
\( \frac{AB}{BD} = \frac{BC}{AB} \)

7. Cross-multiply: To eliminate the fractions, we cross-multiply:
\( AB \cdot AB = BC \cdot BD \)

8. Simplify: This gives us:
\( AB^2 = BC \cdot BD \)

9. Conclusion: Thus, we have proven that:
\( AB^2 = BC \times BD \)