Statement : I,
Assuming LMN is triangle. Assume P, Q are mid points of lines LM, LN. If PQ2=MP2+NQ2 then LMN is Right angled triangle with right angle over L?
Statement : II.
In a triangle ABC if AB2>BC2+CA2 Then ∠ACB is a obtuse angle.
Statement I and Statement II both are correct but statement isa correct explanation for Statement I.
Statement I and Statement II both are correct but Statement II is not a correct explanation for Statement I
Statement I is correct but Statement II is false
Statement I is false but statement II is correct
Step by step video & image solution for Statement : I, Assuming LMN is triangle. Assume P, Q are mid points of lines LM, LN. If PQ^(2)=MP^(2)+NQ^(2) then LMN is Right angled triangle with right angle over L? Statement : II. In a triangle ABC if AB^(2)gtBC^(2)+CA^(2) Then angleACB is a obtuse angle. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In a right angled triangle a2+b2+c2 is :
AR2B4R2C8R2Dnone of theseIn a right angled triangle a2+b2+c2 is :
AR2B4R2C8R2Dnone of theseIn a right angled triangle ABC, the bisector of the right angle C divides AB into segment x and y and tan(A−B2)=t, then x:y is equal to
A(1+t)=(1−t)B(1−t):(t+1)C1:(1+t)D(1−t):1
In △ABC if 2sin2C=2+cos2A+cos2B, then prove that triangle is right angled.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
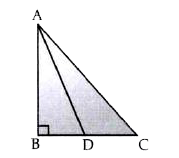
View SolutionIn the given figure ABC is a right angled triangle with ∠B=90∘ . D is the mid -point of BC . Show that AC2=AD2+3CD2 .
View SolutionIf ΔABC is right-angled triangle, then ∑(sin2A) is
View SolutionThe acute angle of right triangle are in the ratio 2:1 .Find each of these angles.
View Solution
