In a quarter circle, a square is in it such that it is placed at equidistant from the adjecent sides of circle. If side of square is x then find the radius of quarter circle?
2x√π
16xπ+4
√2x
√5x√2
To find the radius of the quarter circle in which a square of side length x is inscribed, we can follow these steps:
Step 1: Understand the Geometry
We have a quarter circle with a square inscribed such that it is equidistant from the adjacent sides of the circle. The square's corners touch the arc of the quarter circle.
Step 2: Identify the Relationship Between the Square and the Circle
Since the square is placed such that it is equidistant from the adjacent sides of the quarter circle, we can denote the distance from the center of the quarter circle to the side of the square as d. This distance is equal to x√2 because the diagonal of the square bisects the angle of the quarter circle.
Step 3: Calculate the Diagonal of the Square
The diagonal D of the square can be calculated using the formula:
D=x√2
Step 4: Set Up the Right Triangle
We can visualize a right triangle formed by:
- One leg being the distance from the center of the quarter circle to the side of the square (which is d=x√2),
- The other leg being half the diagonal of the square (which is D2=x√22),
- The hypotenuse being the radius r of the quarter circle.
Step 5: Apply the Pythagorean Theorem
Using the Pythagorean theorem:
r2=(x√2)2+(x√22)2
Step 6: Simplify the Equation
Calculating each term:
(x√2)2=x22
(x√22)2=2x24=x22
Thus, we have:
r2=x22+x22=2x22=x2
Step 7: Find the Radius
Taking the square root of both sides gives us:
r=√x2=x
Conclusion
The radius of the quarter circle is:
r=x√2
We have a quarter circle with a square inscribed such that it is equidistant from the adjacent sides of the circle. The square's corners touch the arc of the quarter circle.
Since the square is placed such that it is equidistant from the adjacent sides of the quarter circle, we can denote the distance from the center of the quarter circle to the side of the square as d. This distance is equal to x√2 because the diagonal of the square bisects the angle of the quarter circle.
The diagonal D of the square can be calculated using the formula:
D=x√2
We can visualize a right triangle formed by:
- One leg being the distance from the center of the quarter circle to the side of the square (which is d=x√2),
- The other leg being half the diagonal of the square (which is D2=x√22),
- The hypotenuse being the radius r of the quarter circle.
Using the Pythagorean theorem:
r2=(x√2)2+(x√22)2
Calculating each term:
(x√2)2=x22
(x√22)2=2x24=x22
Thus, we have:
r2=x22+x22=2x22=x2
Taking the square root of both sides gives us:
r=√x2=x
The radius of the quarter circle is:
r=x√2
Topper's Solved these Questions
Similar Questions
Knowledge Check
The radius of a circle is a side of a square. The ratio of the areas of the circle and the square is
A1:πBπ:1Cπ:2D2:πA square is inscribed in a quarter circle in such a way that two of its adjacent vertices on the radius are equidistant from the centre and other two vertices lie on the circumference. If the side of square is √52 cm, then what is the radius (in cm) of the circle?
A2B2.5C5D10The area of a square is equal to the area of a circle. What is the ratio between the side of the square and the radius of the circle?
A√π:1B1:√3C1:πDπ:1
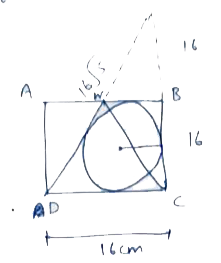
ABCD is a square of side 10 cm . BC is the tangent . Find the radius of circle .
View SolutionABCD is a square . W is the mid point of AB side of square is 16 cm. Find the radius of circle in figure
View SolutionThe sum of the perimeters of a circle and a square is k , where k is some constant. Prove that the sum of their areas is least when the side of the square is double the radius of the circle.
View SolutionThe sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
View SolutionThe areas of a circle and a square are same. The ratio of the side of the square to the radius of the circle is
View Solution
