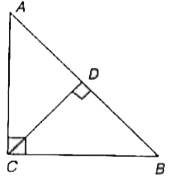
In a right angle triangle $Δ A B C$ a point D is situated on side BC where AB is hypotenuse of triangle. Then, which of the following is correct-

$A B^{2} + C D^{2} = B C^{2} + A D^{2}$

$C D^{2} + B D^{2} = 2 A D^{2}$

$A B^{2} + A C^{2} = 2 A D^{2}$

$A B^{2} = A D^{2} + B D^{2}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the given right triangle $Δ A B C$ where $A B$ is the hypotenuse and point $D$ is located on side $B C$ . We will derive a relationship based on the properties of right triangles.
1. Draw the Triangle:
- Draw triangle $A B C$ such that $∠ C$ is the right angle. Label the sides as follows: $A B$ is the hypotenuse, $A C$ is one leg, and $B C$ is the other leg.
2. Identify Point D:
- Mark point $D$ on side $B C$ .
3. Form Two Right Triangles:
- Recognize that we can form two right triangles: $Δ A C B$ and $Δ A C D$ .
4. Apply the Pythagorean Theorem:
- For triangle $A C B$ :
$A B^{2} = A C^{2} + B C^{2} (Equation 1)$
- For triangle $A C D$ :
$A D^{2} = A C^{2} + C D^{2} (Equation 2)$
5. Express $A C^{2}$ from Both Equations:
- From Equation 1, we can express $A C^{2}$ :
$A C^{2} = A B^{2} - B C^{2} (Equation 3)$
- From Equation 2, we can express $A C^{2}$ as well:
$A C^{2} = A D^{2} - C D^{2} (Equation 4)$
6. Set Equations 3 and 4 Equal:
- Since both expressions equal $A C^{2}$ , we can set them equal to each other:
$A B^{2} - B C^{2} = A D^{2} - C D^{2}$
7. Rearrange the Equation:
- Rearranging gives us:
$A B^{2} - C D^{2} = A D^{2} - B C^{2}$
8. Conclusion:
- This relationship shows how the squares of the segments relate to each other in the context of the right triangle and point $D$ .

Updated on:7/8/2024

In a right angled triangle ABC, CD is the perpendicular on the hypotenuse AB. Which of the following is correct?

A $C D = \frac{A C \times B C}{A B}$
B $A D = \frac{A C \times A C}{A B}$
C $B D = \frac{B C \times B C}{A B}$
DAll of the above
In a $Δ A B C, D$ is a point on BC. AB is the hypotenus of then which relation is correct .
A $A B^{2} + C D^{2} = B C^{2} + A D^{2}$
B $C D^{2} + B D^{2} = 2 A D^{2}$
C $A B^{2} + A C^{2} = 2 A D^{2}$
D $A B^{2} + A D^{2} = B D^{2}$
A point D is taken from the side BC of a right angled triangle ABC, where AB is hypotenuse. Then,
A $A B^{2} + C D^{2} = B C^{2} + A D^{2}$
B $C D^{2} + B D^{2} = 2 A D^{2}$
C $A B^{2} + A C^{2} = 2 A D^{2}$
D $A B^{2} + A D^{2} = B D^{2}$