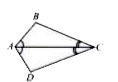
The diagonals of quad. ABCD cut at right angle then find AB2+CD2 = ?
BC2−AD2
BC2+AD2
BC+AD
BC−AD
To solve the problem, we need to find the expression for AB2+CD2 given that the diagonals of quadrilateral ABCD intersect at right angles.
1. Understanding the Quadrilateral and Diagonals:
- Let quadrilateral ABCD be defined with points A, B, C, and D.
- The diagonals AC and BD intersect at point O, forming right angles (90 degrees) at O.
2. Applying the Pythagorean Theorem:
- In triangle AOB, we can apply the Pythagorean theorem:
AB2=AO2+OB2
- In triangle COD, we can also apply the Pythagorean theorem:
CD2=OC2+OD2
3. Combining the Results:
- Now, we can add the two equations derived from the triangles:
AB2+CD2=(AO2+OB2)+(OC2+OD2)
- This simplifies to:
AB2+CD2=AO2+OB2+OC2+OD2
4. Analyzing Other Triangles:
- Next, we analyze triangles BOC and AOD:
- In triangle BOC:
BC2=OB2+OC2
- In triangle AOD:
AD2=AO2+OD2
5. Setting Up the Final Equation:
- Now, we can express AO2+OD2 and OB2+OC2 in terms of AD2 and BC2:
AO2+OD2=AD2
OB2+OC2=BC2
6. Substituting Back:
- Substituting these back into our equation for AB2+CD2:
AB2+CD2=BC2+AD2
Conclusion:
Thus, we conclude that:
AB2+CD2=BC2+AD2
- Let quadrilateral ABCD be defined with points A, B, C, and D.
- The diagonals AC and BD intersect at point O, forming right angles (90 degrees) at O.
- In triangle AOB, we can apply the Pythagorean theorem:
AB2=AO2+OB2
- In triangle COD, we can also apply the Pythagorean theorem:
CD2=OC2+OD2
- Now, we can add the two equations derived from the triangles:
AB2+CD2=(AO2+OB2)+(OC2+OD2)
- This simplifies to:
AB2+CD2=AO2+OB2+OC2+OD2
- Next, we analyze triangles BOC and AOD:
- In triangle BOC:
BC2=OB2+OC2
- In triangle AOD:
AD2=AO2+OD2
- Now, we can express AO2+OD2 and OB2+OC2 in terms of AD2 and BC2:
AO2+OD2=AD2
OB2+OC2=BC2
- Substituting these back into our equation for AB2+CD2:
AB2+CD2=BC2+AD2
Thus, we conclude that:
AB2+CD2=BC2+AD2
Topper's Solved these Questions
Similar Questions
Knowledge Check
Is ||gm ABCD a square?
I. Diagonals of ||gm ABCD are equal.
II. Diagonals of ||gm ABCD intersect at right angles.Aif the question can be answered by one of the given statements alone and not by the other,Bif the quesiton can be answered by either statement alone,Cif the question can be answered by both the statements together but not by any one of the two,Dif the question cannot be answered by using both the statements together.In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)
If the diagonal BD of a quadrillateral ABCD bisects both ∠Band∠D. Prove that ABBC=ADCD.
View SolutionIn a trapezoid ABCD,AB||CD,|AB|=4 and |CD|=10 .Suppose that lines AC and BD intersect at right angle and that lines BC and DA ,when extended to point Q form an angle of 45∘ ,then area of trapezoid ABCD is
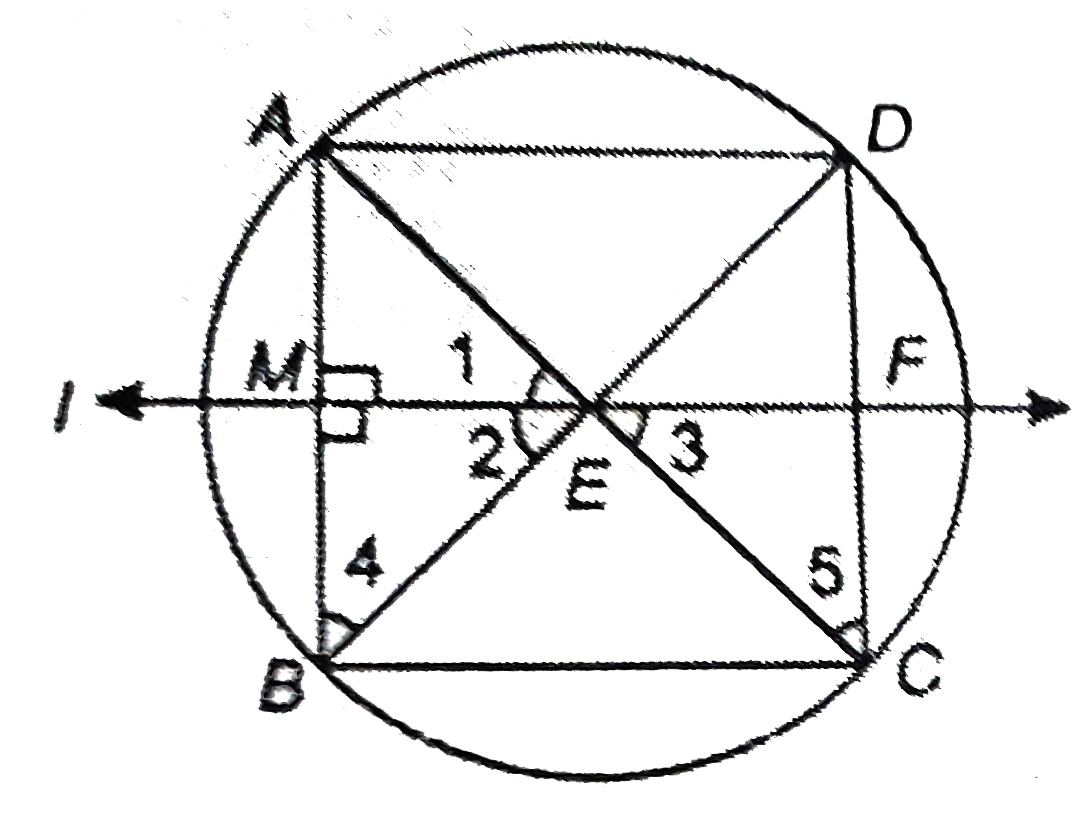
View SolutionThe diagonals AC and BD of a cyclic quadrilateral ABCD interest at right angles at E (figure). A line l drawn through E and perpendicular to AB meets CD at F. Prove that F is the mid-point of CD.
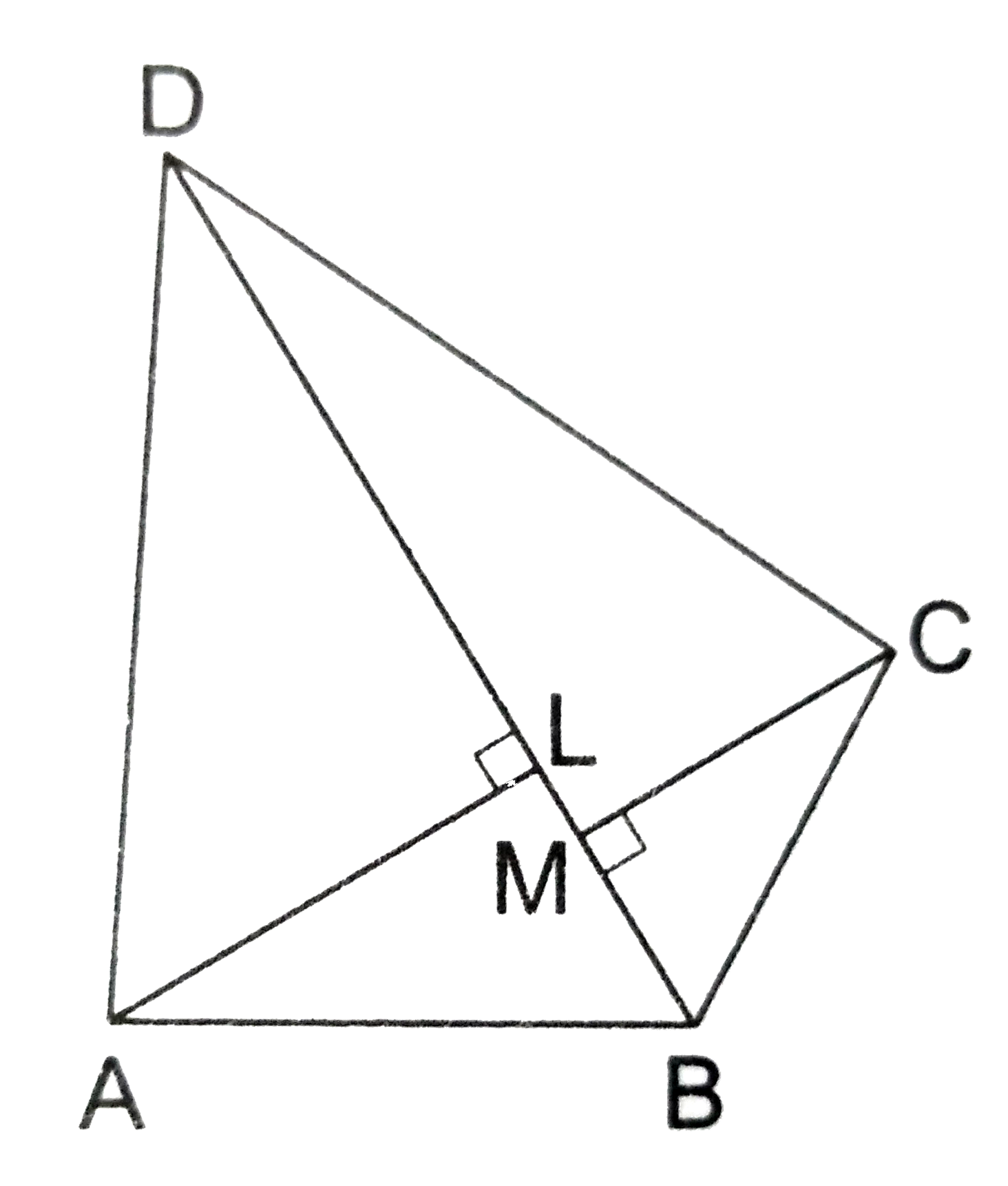
View SolutionBD is one of the diagonals of a quad. ABCD. If AL⊥BDandCM⊥BD, show that
ar(quad. ABCD)=12×BD×(AL+CM).
View SolutionThe diagonals of cyclic quadrilateral ABCD are congruent. Show that AD=BC and seg AB || seg CD.
View Solution