Aline meets the co-ordinate axes in A and B.A circle is circumscribed about the triangle OAB. The distances from the end points of the side AB to the line touching the circle at the origin O are equal to pand g respectively. The diameter of the circle is
p(p+q)
alp+q)
p+q
12(p+q)
The correct Answer is:C
Topper's Solved these Questions
- THE CIRCLE BOOK - ML KHANNACHAPTER - THE CIRCLE EXERCISE - Problem Set (2) (TRUE AND FALSE)
2 Videos
- THE CIRCLE BOOK - ML KHANNACHAPTER - THE CIRCLE EXERCISE - Problem Set (2) (FILL IN THE BLANKS)
6 Videos
- THE CIRCLE BOOK - ML KHANNACHAPTER - THE CIRCLE EXERCISE - Problem Set (1) (FILL IN THE BLANKS)
10 Videos
- TANGENTS AND NORMALSBOOK - ML KHANNACHAPTER - TANGENTS AND NORMALSEXERCISE - SELF ASSESSMENT TEST (MULTIPLE CHOICE QUESTIONS)
19 Videos
- THE ELLIPSEBOOK - ML KHANNACHAPTER - THE ELLIPSEEXERCISE - SELF ASSESSMENT TEST
9 Videos
Similar Questions
A line meets the coordinate axes at A and B . A circle is circumscribed about the triangle OAB. If d1andd2 are distances of the tangents to the circle at the origin O from the points AandB , respectively, then the diameter of the circle is (a)2d1+d22 (b) d1+2d22 (c)d1+d2 (d) d1d2d1+d2
View SolutionA line meets the coordinate axes at A and B . A circle is circumscribed about the triangle OAB. If d1andd2 are distances of the tangents to the circle at the origin O from the points AandB , respectively, then the diameter of the circle is 2d1+d22 (b) d1+2d22 d1+d2 (d) d1d2d1+d2
View Solution
Knowledge Check
A line meets the coordinate axes at A and B. A circle is circumscribed obout the triangle OAB. If the distance of the points A and B from the tangent at O, the origin, to the circle are m and n respectively, find the diameter of the circle.
A2m+n2B(m+n)Cmnm+nDm+2n2A line meets the co-ordinates axes at A(a, 0) and B(0, b) A circle is circumscribed about the triangle OAB. If the distance of the points A and B from the tangent at origin to the circle are 3 and 4 repectively, then the value of a2+b2+1 is
A20B30C40D50A line makes equal intercepts of length a on the coordinate axes. A circle is circumscribed about the triangle which the line makes with the coordinate axes. The sum of the distance of the vertices of the triangle from the tangent to this circle at the origin is
Aa/√2BaCa√2Da+√2
A line meets the co-ordinates axes at A(a, 0) and B(0, b) A circle is circumscribed about the triangle OAB. If the distance of the points A and B from the tangent at origin to the circle are 3 and 4 repectively, then the value of a2+b2+1 is
View SolutionThe sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View SolutionThe straight line x + 2y = 1 meets the coordinate axes at A and B. A circle is drawn through A,B and the origin. Then, the sum of perpendicular distances from A and B on the tangent to the circle at the origin is
View SolutionIn the given figure, G, a point on the circle, is the centroid of the triangle OAB.
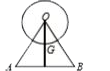
Find the ratio of the area of the equilateral triangle OAB to that of the circle whose centre is O.
View Solution
