The Newton-Raphson method for finding the root of an equation f(x)=0 is
xn+1=xn−f'(xn)f(xn)
xn+1=xn−f(xn)f'(xn)
xn+1=xn+f(xn)f'(xn)
none of these
The correct Answer is:B
Topper's Solved these Questions
- NUMERICAL METHODSBOOK - ML KHANNACHAPTER - NUMERICAL METHODSEXERCISE - SELF ASSESSMENT TEST
10 Videos
- MEASURES OF CENTRAL TENDENCY BOOK - ML KHANNACHAPTER - MEASURES OF CENTRAL TENDENCY EXERCISE - ASSERTION / REASON
1 Videos
- PAIR OF STRAIGHT LINESBOOK - ML KHANNACHAPTER - PAIR OF STRAIGHT LINESEXERCISE - SELF ASSESSMENT TEST
10 Videos
Similar Questions
Knowledge Check
Using Newton-Raphson's method, the approximate value of the root of the equation x4−x−10=0 near to the values 2, correct to three decimal places is
A1.856B1.735C1.674Dnone of theseThe positive root of x2−78.8=0 after first approximation by Newton Raphson method assuming initial approximation to the root is 14, is
A9.821B9.814C9.715D9.915The value of the root nearest to the 2 after first iteration of the equation x4–X−10=0 by Newton-Raphson method
A2.321B2.125C1.983D1.871
The equation whose roots are reciprocals of the roots of the equation f(x)=0 is
View SolutionUsing the combined method find all roots of the equation f(x)≡x3−5x+1=0 accurate to three decimal places.
View SolutionConsider the graph of y = f(x) as shown in the following figure.
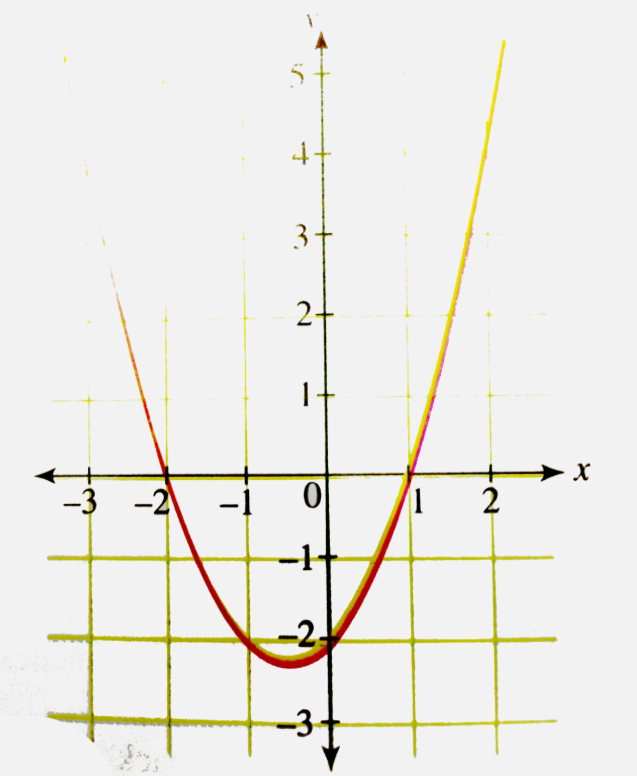
(i) Find the sum of the roots of the equation f (x) = 0.
(ii) Find the product of the roots of the equation f(x) = 4.
(iii) Find the absolute value of the difference of the roots of the equation f(x) = x+2 .
View SolutionConsider the graph of y = f(x) as shown in the following figure.

(i) Find the sum of the roots of the equation f (x) = 0.
(ii) Find the product of the roots of the equation f(x) = 4.
(iii) Find the absolute value of the difference of the roots of the equation f(x) = x+2 .
View SolutionApplying Newton.s method , find the an accuracy up to 0.01 the positive roots of the following equations :
(a) x3+50x−60=0
(b) x3+x−32=0
View Solution
