A particle moves in a straight line with a velocity given by dxdt=x+1 (x is the distance described).
The time taken by the particle to traverse a distance of 99 metres is
log10e
2loge10
2log10e
12log10e
The correct Answer is:B
Step by step video, text & image solution for A particle moves in a straight line with a velocity given by (dx)/(dt)=x+1 (x is the distance described). The time taken by the particle to traverse a distance of 99 metres is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A particle moves in a line with velocity given by dsdt=s+1. The time taken by the particle to cover a distance of 9 metre is (A) 1 (B) log10 (C) 2log10 (D) 10
View SolutionA particle moves in a straight line with a velocity which varies as the square of distance from a fixed point .Its acceleration varies as the cube of the distance .
View Solution
Knowledge Check
- Question 1 - Select One
A partical moves in a straight line with a velocity given by dxdt=x+1 (x is the distance described). The time taken by a particle to traverse a distance of 99 metres, is
Alog10eBloge10C2log10eD12log10e. - Question 2 - Select One
A particle moves in a straight line with a velocity given by dxdt=x+1 (x is the distance described).
The time taken by the particle to traverse a distance of 99 metres isAlog10eB2loge10C2log10eD12log10e - Question 3 - Select One
A particle starts from origin with a velocity (in m/s) given by the equation dxdt=x+1. The time (in second) taken by the particle to traverse a distance of 24 m is
Aln 24Bln 5C2 ln 5D2 ln 4
The velocity v of a particle at any instant t moving in a straight line is given by v=s +1 where s meter is the distance travelled in t second what is the time taken by the particle to cover a distacne of 9m ?
View SolutionA particle moves on a straight line with a uniform velocity. The angular momentum of the particles is
View SolutionA particle moves along a horizontal straight line with a velocity-time relationship as shown in the figure-1.129. The total distance moved by the particle is :
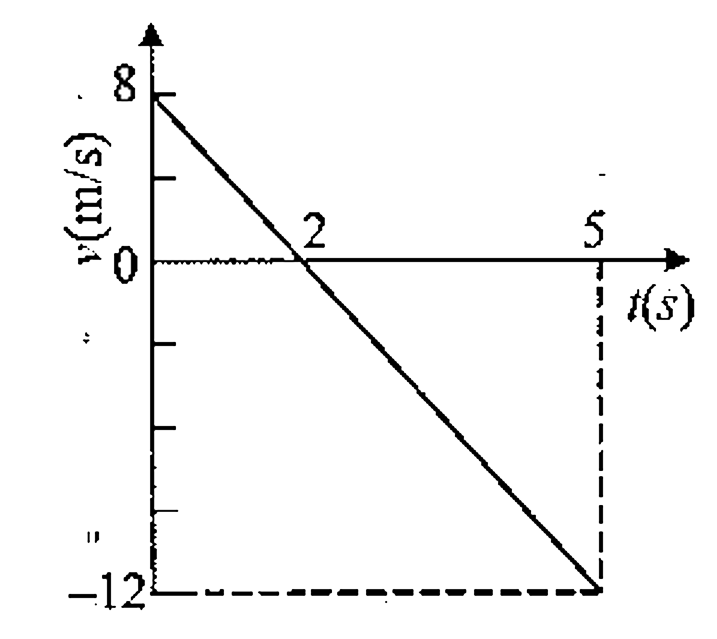 View Solution
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 (where x is its distance from the origin). The acceleration of the particle is
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View Solution

