A given force is resolved into components P and Q equally inclined to it. Then
P=2Q
2P=Q
P=Q
None of these
The correct Answer is:C
To solve the problem of resolving a given force F into components P and Q that are equally inclined to it, we can follow these steps:
Step 1: Understand the Geometry of the Problem
When a force F is resolved into two components P and Q, and both components are equally inclined to the force, it means that the angle between the force and each component is the same. Let's denote this angle as α.
Step 2: Set Up the Relationship Between the Forces
Since P and Q are equally inclined to F, we can express the components in terms of the angle α:
- The horizontal component of F can be expressed as Fcos(α).
- The vertical component of F can be expressed as Fsin(α).
Step 3: Equate the Components
Since both components P and Q are equal and inclined at the same angle α, we can write:
- P=Fcos(α)
- Q=Fsin(α)
Step 4: Use the Property of Equal Angles
Since P and Q are equal, we can set P=Q:
Fcos(α)=Fsin(α)
Step 5: Simplify the Equation
Dividing both sides by F (assuming F≠0):
cos(α)=sin(α)
Step 6: Solve for the Angle
The equation cos(α)=sin(α) implies that:
tan(α)=1
This means:
α=45∘
Step 7: Calculate the Components
Now, substituting α=45∘ back into the equations for P and Q:
P=Fcos(45∘)=F⋅1√2=F√2
Q=Fsin(45∘)=F⋅1√2=F√2
Conclusion
Thus, the components P and Q are both equal to F√2 when the force F is resolved into two equal components that are inclined at 45∘ to the force.
---
When a force F is resolved into two components P and Q, and both components are equally inclined to the force, it means that the angle between the force and each component is the same. Let's denote this angle as α.
Since P and Q are equally inclined to F, we can express the components in terms of the angle α:
- The horizontal component of F can be expressed as Fcos(α).
- The vertical component of F can be expressed as Fsin(α).
Since both components P and Q are equal and inclined at the same angle α, we can write:
- P=Fcos(α)
- Q=Fsin(α)
Since P and Q are equal, we can set P=Q:
Fcos(α)=Fsin(α)
Dividing both sides by F (assuming F≠0):
cos(α)=sin(α)
The equation cos(α)=sin(α) implies that:
tan(α)=1
This means:
α=45∘
Now, substituting α=45∘ back into the equations for P and Q:
P=Fcos(45∘)=F⋅1√2=F√2
Q=Fsin(45∘)=F⋅1√2=F√2
Thus, the components P and Q are both equal to F√2 when the force F is resolved into two equal components that are inclined at 45∘ to the force.
Similar Questions
Two forces of magnitudes P and Q are inclined at an angle (θ). The magnitude of their resultant is 3Q. When the inclination is changed to (180∘−θ), the magnitude of the resultant force becomes Q. Find the ratio of the forces.
View SolutionExplain how a vector can be resolved into its rectangular components in three dimensions.
View Solution
Knowledge Check
A force of 10N is resolved into the perpendiuclar components. If the first component makes 30∘ with the force, the magnitudes of the components are
A5N, 5NB5√2N,5NC5√3N,5ND10N,10√3NContrapositive of given statement p is, where
p : If slope of a straight line is 45∘, then it is equally inclined to both the axesAIf a straight line is equally inclined to both the axes then its siope is 45∘BIf a straight line is equally inclined to both· the axes then its slope is not 45∘CIf a straight line is not equally indinlted to both the axes then its slope is not 45∘DIf a straight line is is not equally inclined to both the axes then its slope is 45∘The given pie diagram represents different components of the soil. Identify P,Q and R and select the correct option
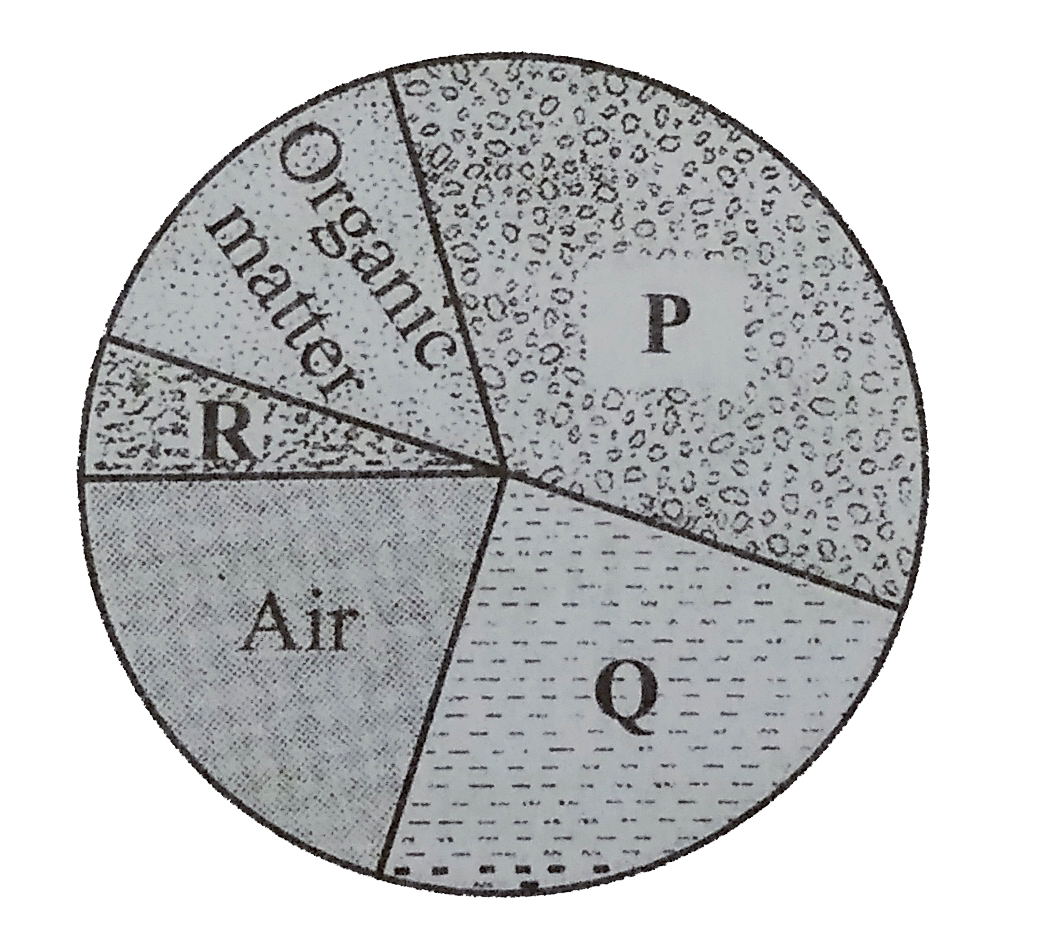 APQRWaterBiotaMineral saltsBPQRMineral saltsBiotaWaterCPQRMineral saltsWaterBiotaDPQRBiotaWaterMineral water
APQRWaterBiotaMineral saltsBPQRMineral saltsBiotaWaterCPQRMineral saltsWaterBiotaDPQRBiotaWaterMineral water
A food sample was tested for the presence of components P, Q, R and S and the following chromatogram was obtained.
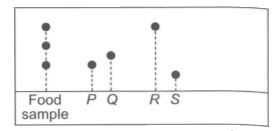
The components not present in food sample are
View SolutionWhen two vectors of magnitudes P and Q are inclined at an angle θ, the magnitudes of their resultant is 2P. When the inclination is changed to 180∘−θ, the magnitudes of the resultant is halved. Find the ratio of P and Q.
View SolutionBlock of mass m is sliding up on the smooth inclined plane with some initial velocity Now on the block match the magnitude value of the forced on 'm' in the given directions (take the component of all the forces in the given direction)

Column -IColumn -II(a)Net force component inhorizontal direction(p) Zero(b)Net force component invertical direction(q)mgsinθcosθ(c)Net force componentalong the inclined plane(r)mgsinθ(d)Net force componentpenpendicular to the inclined plane(s)mg(1−cos2θ)
View SolutionWhat do you mean by rectangular components of a vector ? Explain how a vector can be resolved into two rectangular components in a plane
View SolutionIf the resultant of two forces is equal in magnitude to one of the components and perpendicular to it direction, find the other components using the vector method.
View Solution
