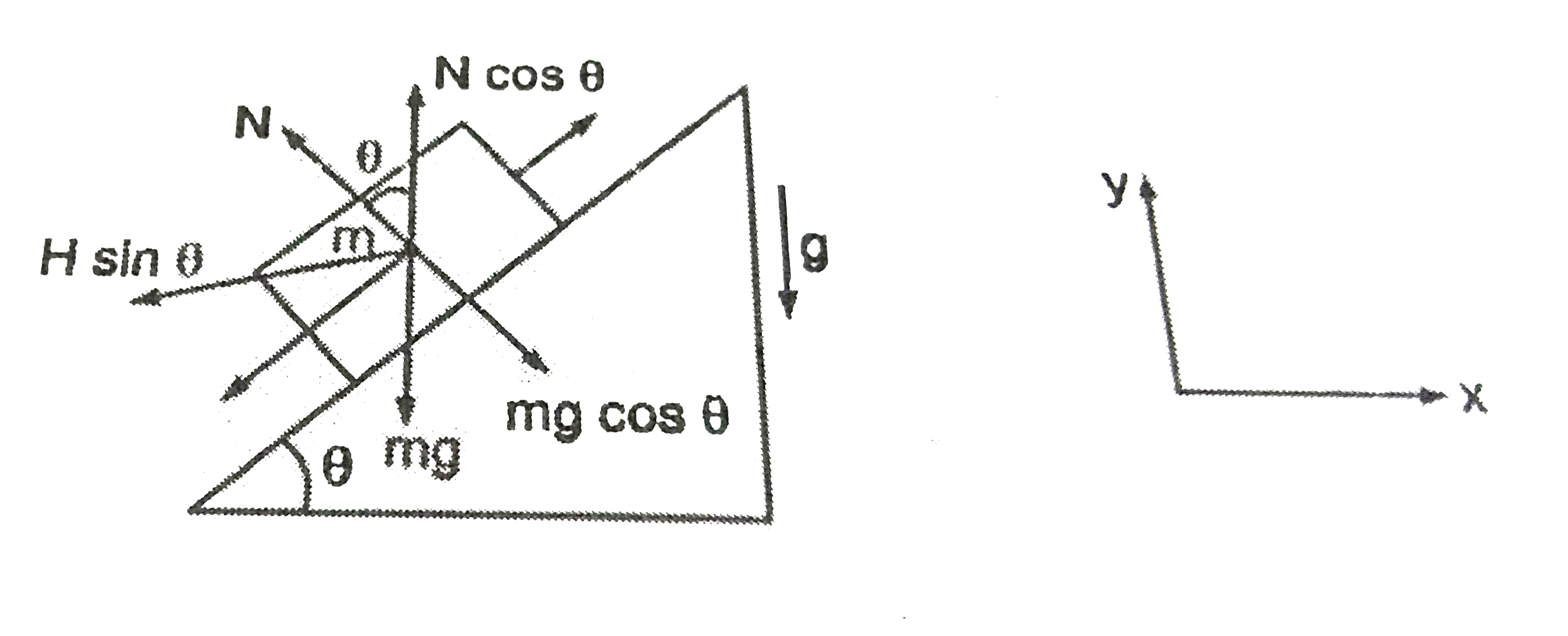
Block of mass m is sliding up on the smooth inclined plane with some initial velocity Now on the block match the magnitude value of the forced on 'm' in the given directions (take the component of all the forces in the given direction)

Column -IColumn -II(a)Net force component inhorizontal direction(p) Zero(b)Net force component invertical direction(q)mgsinθcosθ(c)Net force componentalong the inclined plane(r)mgsinθ(d)Net force componentpenpendicular to the inclined plane(s)mg(1−cos2θ)
The correct Answer is:a→q;b→s;c→r;d→p
Net force in horizontal direction,
FH=mgsinθ.cosθ
Net force in vertical direction
FV=mg−Ncosθ=mg−mgcos2θ
=mg[1−cos2θ]
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Integer question15videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension12videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason4videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice35videos
BASIC MATHEMATICS
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type11videos
FRICTION AND CIRCULAR MOTION
Similar Questions
A force of 10.5 N acts on a particle along a direction making an angle of 370 with the vertical. Find the component of the force in the vertical direction.
View SolutionA block of mass m is thrown upwards with some initial velocity as shown in figure. On the block
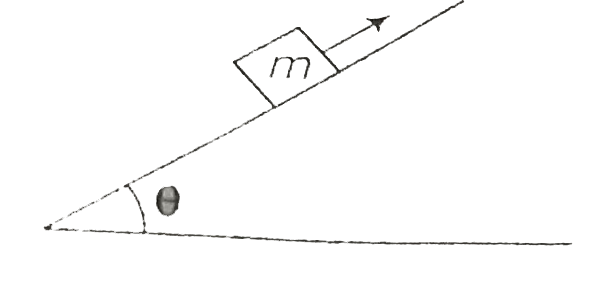
Column IColumn II(A) Net force in horizontal direction(p) Zero(B) Net force in vertical direction(q)m(gsinθ+μgcosθ)(C) Net force along the plane(r)m(gsinθcosθ+μgcos2θ)(D) Net force perpendicular to plane(s)m(gsin2θ+μgsinθcosθ)View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθ - Question 2 - Select One
A block of mass 'M' is slipping down on a rough inclined of inclination α with horizontal with a constant velocity. The magnitude and direction of total reaction from the inclined plane on the block is :
AMgsinα down the inclinedBless than Mgsinα down the inclinedCMg upwardsDMg down wards - Question 3 - Select One
A block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
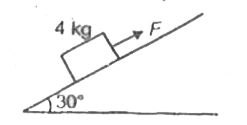 A40 wattB20 wallC60 wattD30 watt
A40 wattB20 wallC60 wattD30 watt
A block of mass m is kept on a smooth moving wedge If the acceleration of the wedge is equal to a, then match the following:
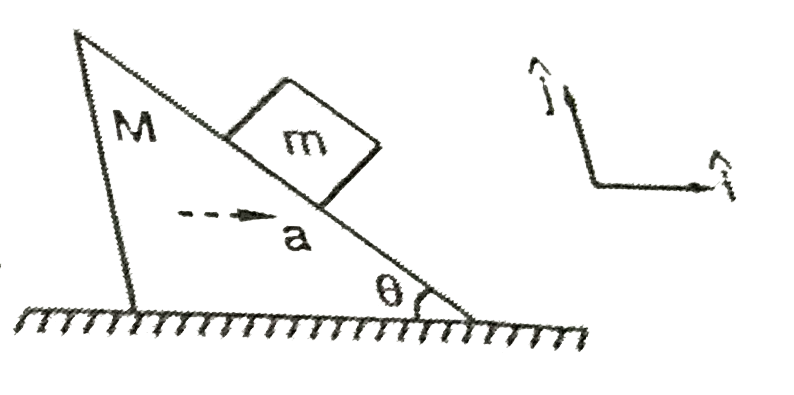
Column -IColumn -II(a)Acceleration of m(p)Ma+m(gcosθ+asinθ)sinθ(b)Acceleration of mrelative to the wedge(q)(gsinθ−acosθ)(c)Force on the wedgeexerted by ground(r)(√g2+a2)sinθ(d)Force on the wedgeexerted by external agent(s)(M+mcos2θ)g+masinθcosθView SolutionA block of mass 10kg is pushed up on a smooth incline plane of inclination 30∘, so that it has acceleration 2m/s2. The applied force is
View SolutionA block of mass m is allowed to slide down a fixed smooth inclined plane of angle q and length l. The magnitude of power developed by the gravitational force when the block reaches the bottom is.
View SolutionA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View SolutionA block of mas m begins to slide down on an inclined plane of inclination θ. The force of friction will be
View Solution

