A triangular lamina ABC right angled at A, rests with its plane vertical and with the sides AB, AC supported by smooth fixed pegs, D,E in a horizontal line. The inclination θ of AC to the horizon is given by ACcosθ−Absinθ=3DEcos2θ.
The correct Answer is:T
Similar Questions
A uniform rectangular board rests vertically in equilibrium with its sides 2a and 2b on two smooth pegs in the same horizontal line distant c apart. Prove that the side of length b makes with the horizontal an angle θ given by c cos2θ=bcosθ−asinθ.
View SolutionIn the given figure if AB=AC then find θ.
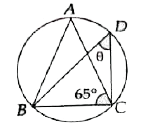
View Solution
Knowledge Check
sin3θsinθ−cos3θcosθ= A)sin2θB)cos4θC)1D)2
Asin2θBcos4θC1D2AB is a vertical diameter of a circle, whose plane is vertical and PQ is a diameter inclined at an angle θ to AB. If the time of sliding down PQ be twice that of sliding down AB, then cosθ=
A12B13C14DNone
Evaluate ∫(2sinθ+sin2θ)dθ(cosθ−1)√cosθ+cos2θ+cos3θ.
View SolutionEvaluate ∫(2sinθ+sin2θ)dθ(cosθ−1)√cosθ+cos2θ+cos3θ.
View SolutionIf →a and →b are unit vectos inclined at an angle θ then the value of ∣∣→a−→b∣∣ is a.2sinθ2 b. 2sinθ c. 2cosθ2 d. 2 cos
View SolutionEquation of the line passing through the point (acos3θ,asin3θ) and perpendicular to the line xsecθ+ycosθ=a is
xcosθ−ysinθ=asin2θ.
View SolutionFind the fix point through which the line (2cosθ+3sinθ)x+(3cosθ−5sinθ)y−(5cosθ−2sinθ)=0 passes for all values of θ
View SolutionIn a triangle ABC, if the median AD makes an angle θ with ACandAB=2AD then sinθ=
View Solution
