A solid right circular cone has its base scooped out removed in sich a way that the hollow is also right circular cone on the same base. The solid cone should be scooped out . . . . . . . .so that the C.G. of the remainder is at the vertex of the hollow cone.
The correct Answer is:one-third
Similar Questions
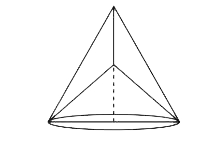
A uniform solid right circular cone has its base cut out in conical shape shown in fig 4E.32 (a) such that the hollow is a right circular cone on the same base. Find centre of mass of the remaining portion may coincide the vertex of the hollow part.

View SolutionA uniform solid right circular cone has its base cut out in conical shape shown in figure such that the hollow portion is a right circular cone on the same base. Find what should be the height of the hollow portion so that the centre of mass of the remaining portion may coincide with the vertex of the hollow portion.
View Solution
Knowledge Check
A uniform solid right circular cone has its base cut out in conical shape shown in figure such that the hollow portion is a right circular cone on the same base. Find what should be the height of the hollow portion so that the centre of mass of the remaining portion may coincide with the vertex of the hollow portion.
 Ah3Bh4C2h3Dh6
Ah3Bh4C2h3Dh6The radius of the base and the height of a right circular cone are doubled. The volume of the cone will be
A8 times of the previous volumeBthree times of the previous volumeC3√2 times of the previous volumeD6 times of the previous volumeThe ratio of the volumes of a right circular cylinder and a right circular cone of the same base and the same height will be
A1:3B3:1C4:3D3:4
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is:
View SolutionBase a right circular cone has a plane end which is in circular shape. This is called the base of the cone.
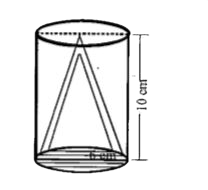
View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the the same height and same base is removed . find the volume of the remaining solid
View SolutionA solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base . The ratio of the volume of the smaller cone to the whole cone is
View SolutionA right circular cone has a volume of 24π cubic inches. If the height of the cone is 2 inches, what is the radius, in inches, of the base of the cone?
View Solution
