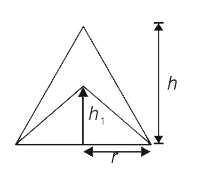
A uniform solid right circular cone has its base cut out in conical shape shown in figure such that the hollow portion is a right circular cone on the same base. Find what should be the height of the hollow portion so that the centre of mass of the remaining portion may coincide with the vertex of the hollow portion.

A

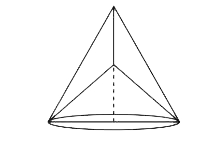
$\frac{h}{3}$

B

$\frac{h}{4}$

C

$\frac{2 h}{3}$

D

$\frac{h}{6}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$M = ρ \frac{1}{3} π r^{2} h, Y_{C M} = \frac{h}{4} [Before removed)$
$M = ρ \frac{1}{3} π r^{2} h_{1}, Y_{1_{C M}} = \frac{h_{1}}{4} [For removed part)$
$Y_{C M} = h_{1} = \frac{M_{Y} - M_{1} Y_{1}}{M - M_{1}}$
$= \frac{ρ \frac{1}{3} π r^{2} (\frac{h^{2}}{4} - \frac{h_{1}^{2}}{4})}{ρ \frac{1}{3} π r^{2} (h - h_{1})} \Rightarrow h_{1} = \frac{h_{1} + h}{4} \Rightarrow h_{1} = \frac{h}{3}$

|

Updated on:21/07/2023

Class 12 PHYSICS ENERGY & MOMENTUM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If a right circular cone has a lateral surface area of $6 π$ and a slant height of 6, what is the radius of the base ?
A $0.50$
B $0.75$
C $1.00$
D $1.25$
Question 2 - Select One
A right circular cone has a volume of $24 π$ cubic inches. If the height of the cone is 2 inches, what is the radius, in inches, of the base of the cone?
A $2 \sqrt{3}$
B6
C12
D36

VMC MODULES ENGLISH-ENERGY & MOMENTUM-LEVEL - 2

Home
Ask Doubt
Profile