A ladder whose centre of gravity divides its length in the ratio a : b is in limting equilibrium with its one end on a rough floor (coefficient of friction μ) and the other end against a rough vertical wall (coefficient of friction μ) .Determine the angle of inclination of the ladder in terms of two angles of friction .
The correct Answer is:=a−bμμμ(a+b)
Topper's Solved these Questions
- RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEBOOK - ML KHANNACHAPTER - RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEEXERCISE - COMPREHENSION
11 Videos
- TANGENTS AND NORMALSBOOK - ML KHANNACHAPTER - TANGENTS AND NORMALSEXERCISE - SELF ASSESSMENT TEST (MULTIPLE CHOICE QUESTIONS)
19 Videos
Similar Questions
A uniform ladder is placed against a wall, if the ground and wall are equally rough the coefficient of friction being tanθ limiting inclination of the ladder to the vertical is 2θ.
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View Solution
Knowledge Check
A uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
Atan−1μBcot−1μCcot−1(2μ)Dtan−1(2μ)A uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
Atan−1μBcot−1μCcot−1(2μ)Dtan−1(2μ)A uniform ladder rests in limiting equilibrium, its lower end on a rough horizontal plae and its upper end against a smooth vertical wall. If θ is the engle of inclination of the ladder to the vertical wall and μ is the coefficient of friction then tanθ is equal to
AμB2μC3μ/2Dμ+1
A body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionAngle of repose for a rough inclined plan is 60∘ The coefficient of friction is.
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionA block pressed against the vertical wall is in equilibrium. The minimum coefficient of friction is:
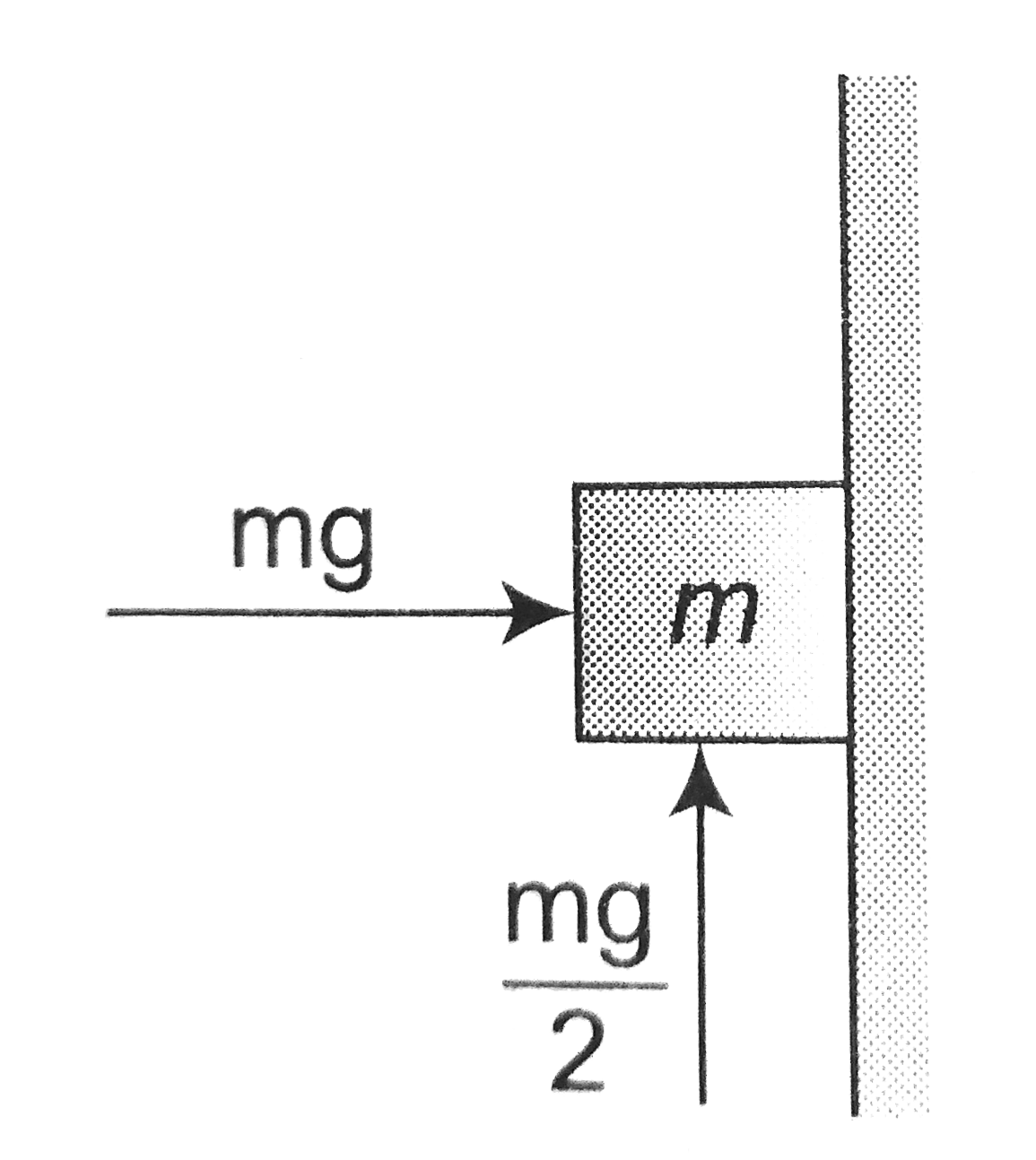
View SolutionA block pressed against the vertical wall is in equilibrium. The minimum coefficient of friction is:

View Solution
