What is the angle between the reflected ray if the angle of incidence is equal to angle of polarisation ?
90∘ i.e., they are mutually perpendicular.
Similar Questions
Knowledge Check
What are the laws of reflection?
(i) The angle of incidence is equal to the angle of reflection, and
(ii) The incident ray, the normal to the mirror at the point of incidence and the reflected ray, all lie in the same plane.
(iii) Incident ray is equal to emergent ray.
(iv) Reflected ray is equal to emergent ray.A(i) and (ii)B(i) and (iv)C(i), (ii) and (iv)DAll the aboveA light ray incidents at an angle 'i' on a plane mirror and undergoes reflection. Arrange the following steps in sequential order to calculate the angle of deviation of the light ray.
(A) The angle between the incident ray and the extended light ray is 180∘ (B) In case of reflection, the angle of incidence (i) is equal to the angle of reflection (r). Then, the angle between the incident ray and the reflected ray is 2i. (C) Draw an imaginary line, extending the incident light ray, which represents the actual path of the light ray. (D) The angle of deviation is the angle between the reflected light ray and the actual path of the light ray, i.e., 180∘−2iABADCBBCADCBACDDCBDAA light ray incidents at an angle 'l' on a plane mirror and undergoes reflection. Arrange the following steps in sequential order to calculate the angle of deviatino of the light ray.
The angle between the incident ray and the extended light ray is 180∘.
In case of reflection, the angle of incidence (i) is equal to the angle of reflection (r). Then the angle between the incident ray and the reflected ray is 2i.
Draw an imaginary line, extending the incident light ray, which reprsesnts the actual path of the light ray.
The angle of deviation is the angle between the reflected light ray and the actual path of the light ray, i.e., 180∘−2i.ABADCBBCADCBACDDCBDA
The angle between incident ray and reflected ray is 60°. What is the value of angle of incidence?
View SolutionIn the figure given the angle between incident ray and the reflected ray is 70∘
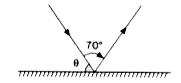
Find the angle of incidence.
View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View SolutionIf the angle between incident ray and reflected ray is 120∘, what is the angle of incidence ?
View Solution
