A cell first connected across 5Ω resistance develops a potential difference of 1.25 V across it. Same cell again connected across 2Ω resistance develops 1V potential difference across it find emf of cell
5 V
15 V
7 V
4 V
To solve the problem, we will use the concept of Ohm's law and the formula for the potential difference across a resistor in a circuit involving a cell with internal resistance.
1. Identify the Given Values:
- When connected across a 5Ω resistor, the potential difference (V1) is 1.25V.
- When connected across a 2Ω resistor, the potential difference (V2) is 1V.
2. Calculate the Current in Each Case:
- For the 5Ω resistor:
I1=V1R1=1.25V5Ω=0.25A
- For the 2Ω resistor:
I2=V2R2=1V2Ω=0.5A
3. Set Up the Equations Using the Formula:
- The formula relating the EMF (E), potential difference (V), current (I), and internal resistance (r) is:
V=E−I⋅r
- For the first case (5 Ω):
1.25=E−0.25⋅r(Equation 1)
- For the second case (2 Ω):
1=E−0.5⋅r(Equation 2)
4. Rearranging the Equations:
- From Equation 1:
E=1.25+0.25r(Equation 3)
- From Equation 2:
E=1+0.5r(Equation 4)
5. Equate the Two Expressions for E:
- Set Equation 3 equal to Equation 4:
1.25+0.25r=1+0.5r
6. Solve for r:
- Rearranging gives:
1.25−1=0.5r−0.25r
0.25=0.25r
r=1Ω
7. Substitute r Back to Find E:
- Substitute r back into either Equation 3 or Equation 4. Using Equation 3:
E=1.25+0.25⋅1=1.25+0.25=1.5V
Final Answer:
The EMF of the cell is 1.5V.
- When connected across a 5Ω resistor, the potential difference (V1) is 1.25V.
- When connected across a 2Ω resistor, the potential difference (V2) is 1V.
- For the 5Ω resistor:
I1=V1R1=1.25V5Ω=0.25A
- For the 2Ω resistor:
I2=V2R2=1V2Ω=0.5A
- The formula relating the EMF (E), potential difference (V), current (I), and internal resistance (r) is:
V=E−I⋅r
- For the first case (5 Ω):
1.25=E−0.25⋅r(Equation 1)
- For the second case (2 Ω):
1=E−0.5⋅r(Equation 2)
- From Equation 1:
E=1.25+0.25r(Equation 3)
- From Equation 2:
E=1+0.5r(Equation 4)
- Set Equation 3 equal to Equation 4:
1.25+0.25r=1+0.5r
- Rearranging gives:
1.25−1=0.5r−0.25r
0.25=0.25r
r=1Ω
- Substitute r back into either Equation 3 or Equation 4. Using Equation 3:
E=1.25+0.25⋅1=1.25+0.25=1.5V
The EMF of the cell is 1.5V.
Similar Questions
In an electric circuit, a call of certain emf provides a potential difference of 1.25 V across a load resistance of 5Ω However, it provides a potential difference of 1 V across a load resistance of 2Ω .The emf of the cell is given by x10V. Then the value of x is ____.
View SolutionA cell of emf 'E' is connected across a resistance R.The potential difference between the terminals of the cell is found to be "V" .The internal resistance of the cell must be:
View Solution
Knowledge Check
The potential difference across terminals of cell of 20 V and r=2Ω connected to 8Ω external resistance is
A16B1.6C160D5v31
A2(E−V)VrB2(E−V)rEC(E−V)rVD(E−V)rA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
AEBE/2CE/4D3/2
Find potential difference across the resistance 300Ω in A and B.
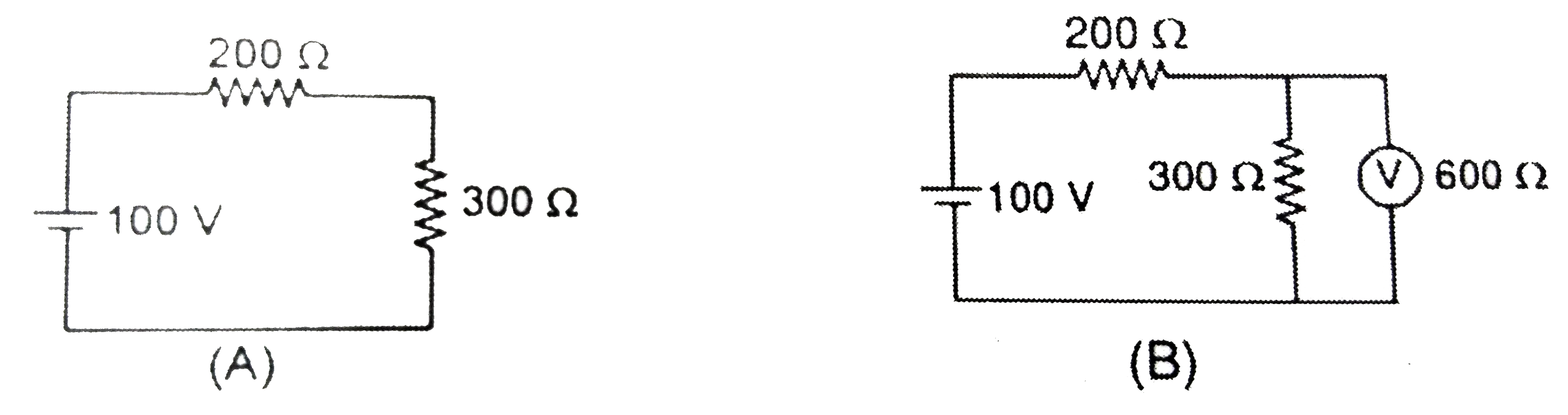
View SolutionFind potential difference across the resistance 300 Ω in A and B.
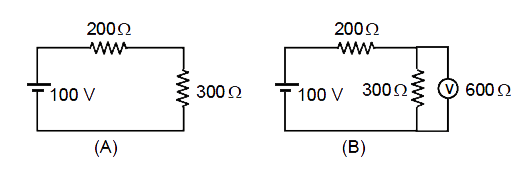
View SolutionA cell has an emf 1.5V. When connected across an external resistance of 2Ω, the terminal potential difference falls to 1.0V. The internal resistance of the cell is:
View SolutionWhat will be the heat produced each second in a 4Ω resistance connected across a potential difference of 20V?
View SolutionWhat will be the heat produced each second in a 4Ω resistance connected across a potential difference of 20V?
View Solution
