In an electric circuit, a call of certain emf provides a potential difference of 1.25 V across a load resistance of 5Ω However, it provides a potential difference of 1 V across a load resistance of 2Ω .The emf of the cell is given by x10V. Then the value of x is ____.
To solve the problem, we need to analyze the circuit conditions given for the two different load resistances and the corresponding potential differences.
1. Understanding the Circuit:
- We have a cell with an EMF (E) and an internal resistance (r).
- When connected to a load resistance (R), the potential difference (V) across the load can be expressed using Ohm's law and Kirchhoff's voltage law.
2. Setting Up the Equations:
- For the first case with a load resistance of 5Ω and a potential difference of 1.25V:
V1=E−I⋅r
where I is the current through the circuit. The current can also be expressed as:
I=ER+r=E5+r
Thus, we can write:
1.25=E−I⋅r=E−(E5+r)⋅r
Rearranging gives us:
1.25=E−E⋅r5+r
Multiplying through by 5+r:
1.25(5+r)=E(5+r)−E⋅r
Simplifying leads to:
1.25⋅5+1.25r=5E
This is our Equation 1.
3. Second Case:
- For the second case with a load resistance of 2Ω and a potential difference of 1V:
V2=E−I′⋅r
where I′=E2+r. Thus:
1=E−(E2+r)⋅r
Rearranging gives:
1=E−E⋅r2+r
Multiplying through by 2+r:
1(2+r)=E(2+r)−E⋅r
Simplifying leads to:
2+r=2E
This is our Equation 2.
4. Solving the Equations:
- From Equation 1:
6.25+1.25r=5E(1)
- From Equation 2:
r=2E−2(2)
- Substitute Equation (2) into Equation (1):
6.25+1.25(2E−2)=5E
Expanding gives:
6.25+2.5E−2.5=5E
Simplifying leads to:
3.75=5E−2.5E
Thus:
3.75=2.5E⟹E=3.752.5=1.5V
5. Finding x:
- The EMF of the cell is given as x10V.
- Since we found E=1.5V:
1.5=x10⟹x=1.5×10=15
Final Answer:
The value of x is 15.
- We have a cell with an EMF (E) and an internal resistance (r).
- When connected to a load resistance (R), the potential difference (V) across the load can be expressed using Ohm's law and Kirchhoff's voltage law.
- For the first case with a load resistance of 5Ω and a potential difference of 1.25V:
V1=E−I⋅r
where I is the current through the circuit. The current can also be expressed as:
I=ER+r=E5+r
Thus, we can write:
1.25=E−I⋅r=E−(E5+r)⋅r
Rearranging gives us:
1.25=E−E⋅r5+r
Multiplying through by 5+r:
1.25(5+r)=E(5+r)−E⋅r
Simplifying leads to:
1.25⋅5+1.25r=5E
This is our Equation 1.
- For the second case with a load resistance of 2Ω and a potential difference of 1V:
V2=E−I′⋅r
where I′=E2+r. Thus:
1=E−(E2+r)⋅r
Rearranging gives:
1=E−E⋅r2+r
Multiplying through by 2+r:
1(2+r)=E(2+r)−E⋅r
Simplifying leads to:
2+r=2E
This is our Equation 2.
- From Equation 1:
6.25+1.25r=5E(1)
- From Equation 2:
r=2E−2(2)
- Substitute Equation (2) into Equation (1):
6.25+1.25(2E−2)=5E
Expanding gives:
6.25+2.5E−2.5=5E
Simplifying leads to:
3.75=5E−2.5E
Thus:
3.75=2.5E⟹E=3.752.5=1.5V
- The EMF of the cell is given as x10V.
- Since we found E=1.5V:
1.5=x10⟹x=1.5×10=15
The value of x is 15.
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - A)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - B)
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
A cell first connected across 5Ω resistance develops a potential difference of 1.25 V across it. Same cell again connected across 2Ω resistance develops 1V potential difference across it find emf of cell
View SolutionIn the given circuit , the potential difference across the capacitor is 12 V. Each resistance is of 3Ω. The cell is ideal. The emf of the cell is
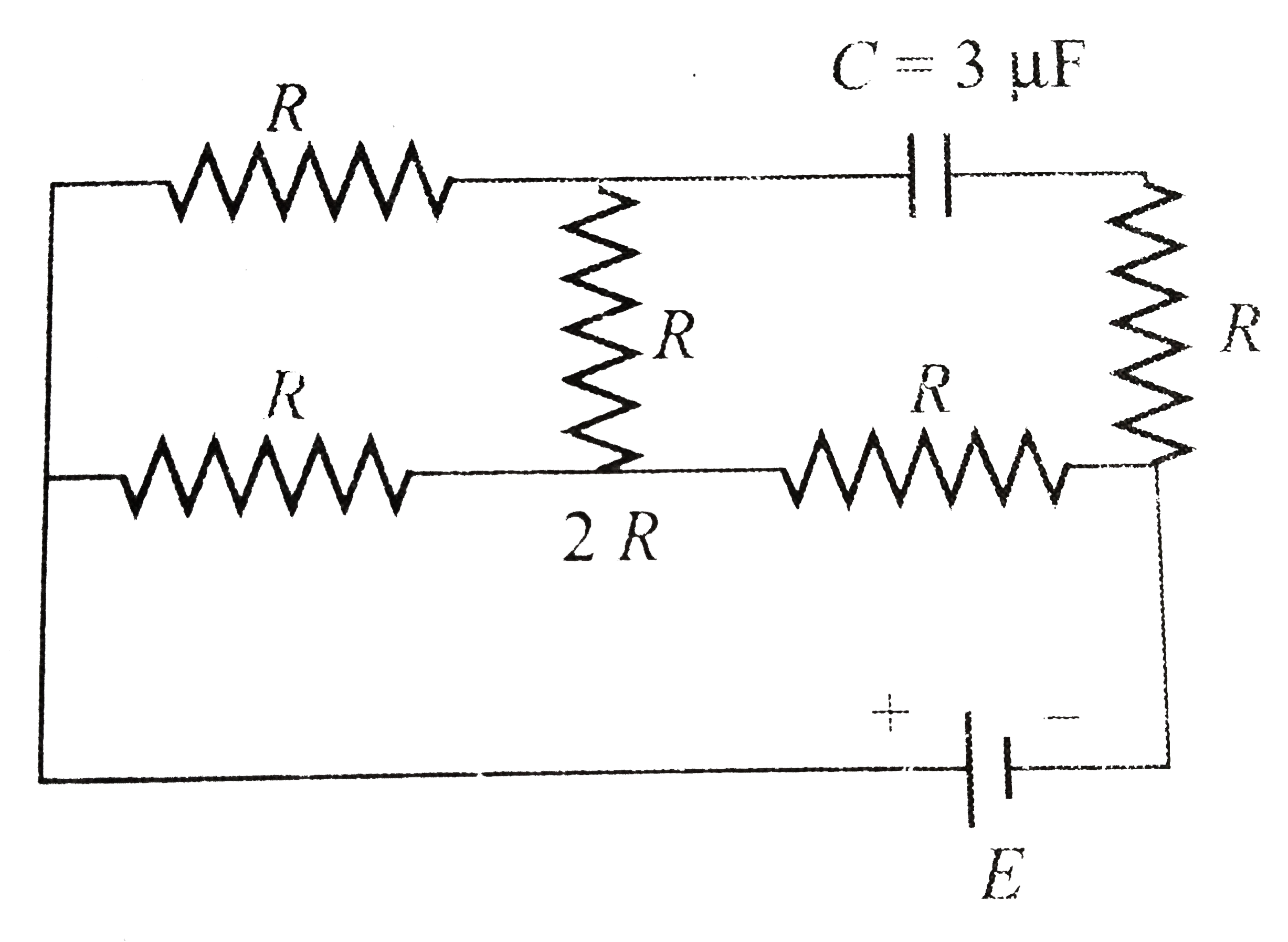
View Solution
Knowledge Check
In the given circuit diagram, potential difference across 2Ω resistance is
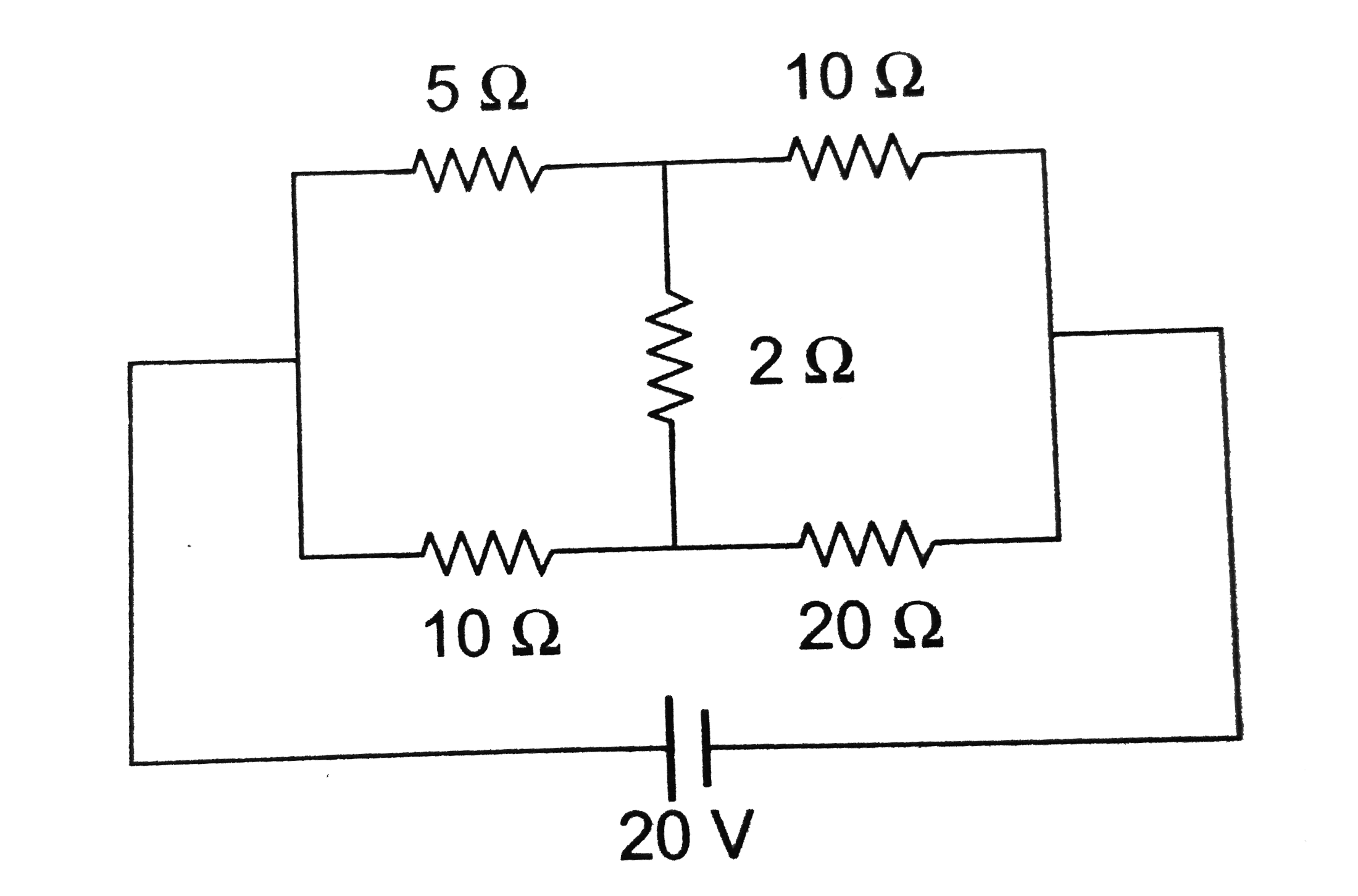 A4VB6VC20VDzero
A4VB6VC20VDzeroA cell has an emf 1.5V. When connected across an external resistance of 2Ω, the terminal potential difference falls to 1.0V. The internal resistance of the cell is:
A2ΩB1.52ΩC1.0ΩD0.5ΩIn the circuit the potential difference across the capacitor is 10V. Each resistance is of 3Ω The cell is ideal. The emf of the cell is
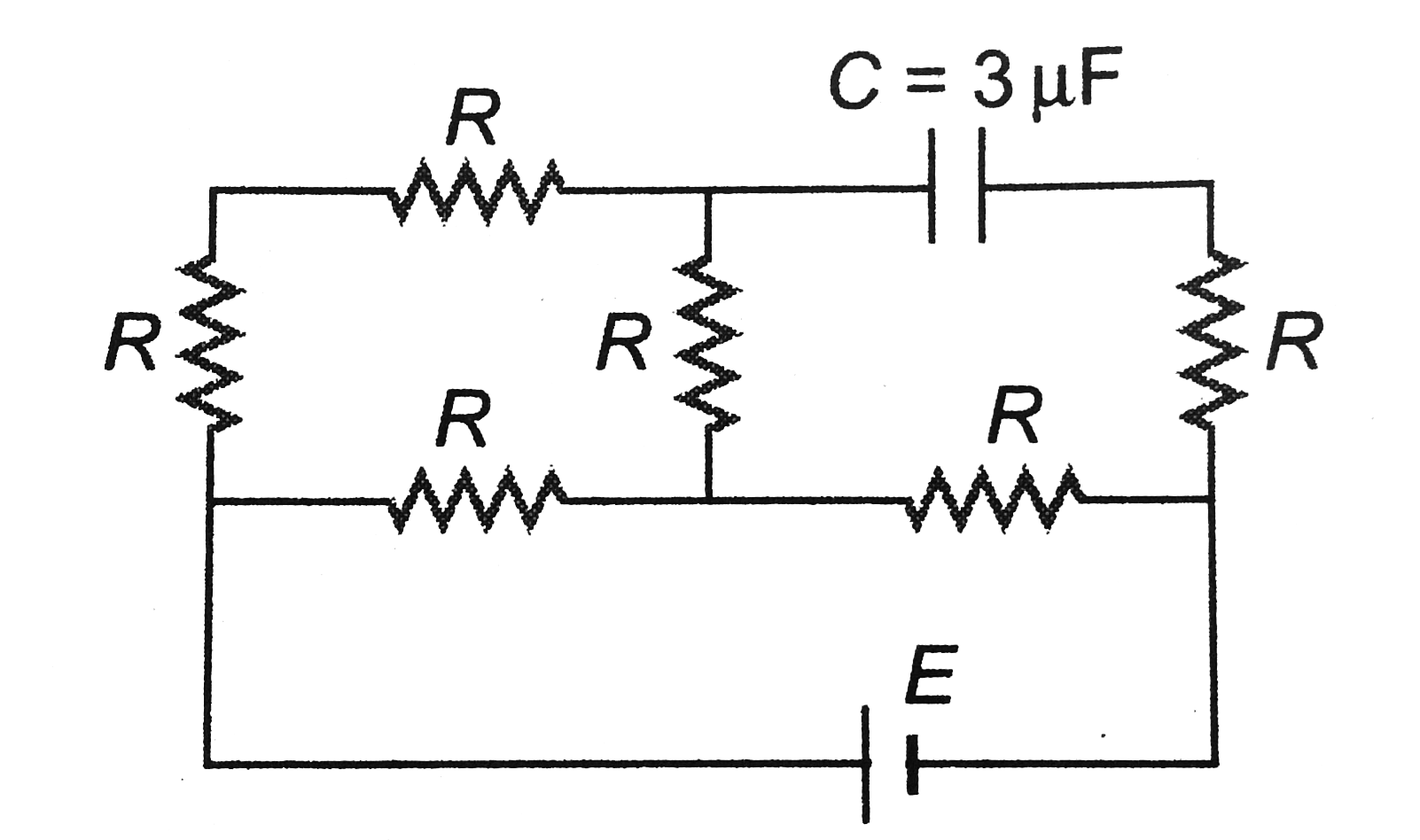 A14VB16VC18VD24V
A14VB16VC18VD24V
In the given circuit, the potential difference across the capacitor is 12V. Each resistance is of 3Ω. The cell is ideal. The emf of the cell is
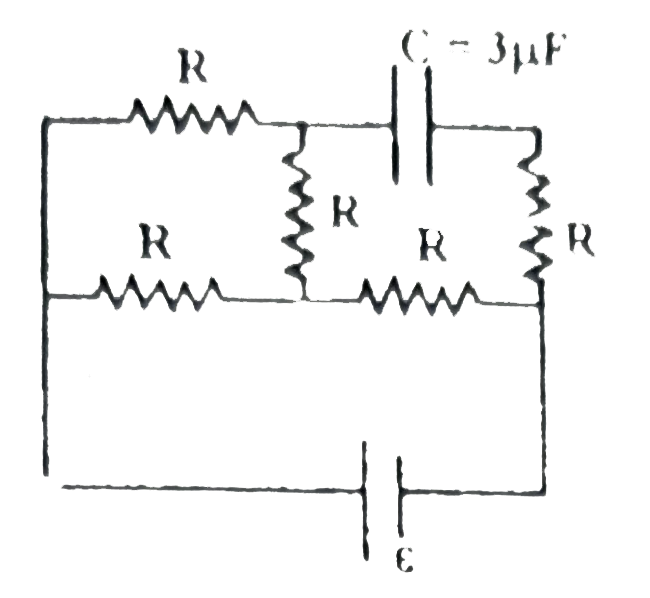
View SolutionA cell of emf 1.5 V is connected with an external resistance 20Ω. The potential difference falls to 1.0 V. The internal resistance of cell is
View SolutionA cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
View SolutionA cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
View SolutionA voltmeter has a resistance of 50Ω is connected across a cell of e.m.f. 2V and internal resistance 10Ω. The reading of voltmeter is
View Solution