State principle of superposition of charges and using it find an expression for force acting at a point charge due to assembly, of 'n' point charges.Solution in Punjabi

Video Solution

Text Solution

Verified by Experts

Principle of superposition of charges : According to this principle when a number of point charges interact in space then total force on a particular charge is the vector sum of forces exerted on it by all the other individual charges.
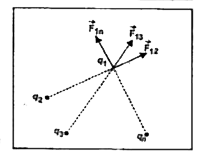
Consider that n point charges $q_{1}, q_{2}, q_{3}, ... ... . . q_{n}$ are distributed in space in a discrete manner. The charges are interacting with each other. Let us find the total force on charges say $q_{1}$ due the all other remaining charges. If the charges $q_{2}, q_{3}, ... ... q_{n}$ exert forces ${\to F}_{12}, {\to F}_{13}, ... ... {\to F}_{1 n}$ on the charge $q_{1}$ , then, according to principle of uperposition, the total force on charge $q_{1}$ given by
${\to F}_{1} = {\to F}_{12} + {\to F}_{13} + ... ... {\to F}_{1 n} ... . (i)$
If the distance between the charges $q_{1} and q_{2}$ is $r_{12}$ , and ${ˆ r}_{21}$ is unit vector from charges $q_{2} and q_{2}$ , then
${\to F}_{12} = \frac{1}{4 π \in_{0}} . \frac{q_{1} q_{2}}{r_{12}} {ˆ r}_{21}$
Similarly, the force on charge $q_{1}$ due to other charges is given by
${\to F}_{13} = \frac{1}{4 π \in_{0}} . \frac{q_{1} q_{2}}{r_{13}} {ˆ r}_{31}$
...............
................
and ${\to F}_{1 n} = \frac{1}{4 π \in_{0}} . \frac{q_{1} q_{n}}{r_{1 n}^{2}} {ˆ r}_{n 1}$
Hence, in equation (i), setting the values of ${\to F}_{12}, {\to F}_{13}, ... ... . . {\to F}_{1 n}$ the total force on charge $q_{1}$ due to all other charges is given by
${\to F}_{1} = \frac{1}{4 π \in_{0}} (\frac{q_{1} q_{2}}{r_{12}^{2}} {ˆ r}_{21} + \frac{q_{1} q_{3}}{r_{13}^{2}} {ˆ r}_{21} + ... . . \frac{q_{1} q_{2}}{r_{1 n}^{2}} {ˆ r}_{n t})$
or ${\to F}_{1} = \frac{1}{4 π \in_{0}} n \sum i = 1, j = 1, in \neq j \frac{q_{i} q_{j}}{r_{i j}^{2}} {ˆ r}_{j i}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND ELECTROSTATIC FORCE

Topper's Solved these Questions

Similar Questions

BETTER CHOICE PUBLICATION-ELECTRIC CHARGES AND ELECTROSTATIC FORCE -LONG ANSWER TYPE QUESTIONS

Home
Ask Doubt
Profile