Question

Using Ampere's circuital law, derive an expression for the magnetic field along the axis of a toroidal solenoid.

Explanation

Ampere.s Circuital Law : This law states that line integral of magnetic field over a closed circuit is equal to Ho (absolute permeability of free space) times the current threading through that circuit.
`oint vecB . vec(dl) = mu_0 I`
Magnetic field due to a Current Carrying Solenoid : A long insulated. wire tightly wound in the form of a helix is known as solenoid.
Each turn of the solenoid can be regarded as a circular loop. Magnetic field due to the whole solenoid will be equal to vector sum of magnetic field of each turn.
Consider a long current carrying solenoid through which current l is flowing and have a number of turns per unit length.

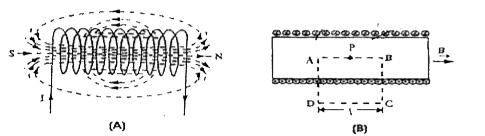
Magnetic field inside the solenoid is uniform and is directed along the axis of the solenoid. Outside the solenoid magnetic field is very weak and can be considered as zero.
Consider a point P well inside a solenoid. Suppose a rectangular current loop ABCD passing through point P as shown in fig. above.
Line integral of magnetic field over a closed rectangular loop ABCD is given as
`oint vecB. vec(dl) = int_A^B vecB. vec(dl) + int_B^C vecB. vec(dl) + int_B^C vecB. vec(dl) + int_D_A vecB. vec(dl)`
But `int_C^B B.vec(dl) = 0 " "` [`because` Outside the solenoid magnetic field is zero]
Also `int_B^C B.vec(dl) = int_D^A vecB. vec(dl) = 0`
`because` For the paths BC and AD, `vecB _|_ vecdl`
`implies oint vecB. vec(dl) = int_A^B vecB . vec(dl) = int_A^B Bdl cos theta`
`because` For path `AB, vecB` and `vec(dl)` are in same direction and hence angle between them is zero.
`oint vecB. vec(dl) = B int_A^B dl`
`= ` B (Length of path AB)
`oint vecB . vec(dl) =Bl`
n = Number of turns per unit length of the solenoid
n (Length of loop ABCD)= nl = Number of turns in the loop ABCD.
According to Ampere.s circuital law
`oint vecB. vec(dl) = mu_0` (Number of turns in loop ABCD) I
`Bl = mu_0 (nl) I ` [Using egn. (1)]
`B = mu_0 nI`
If N = Total number of turns in the solenoid,
then `n = N/l` are hence
`B = mu_0 N/l I`
which is the required expression for the magnetic field at point well inside the solenoid and this field acts along the axis of the solenoid.