Write expression for the magnetic flux density at a point due to a current carrying wire of:
an infinite length?Solution in Punjabi
Consider a long straight wire LM.
Let I = Current flowing through the wire from L to M.
Let P be the observation point, where we want to calculate the magnetic field.
OP = a = Perpendicular distance of P from the current carrying wire
Consider the small element CD of length dl of the wire and I is distance of mid-point of elementary portion CD from O.
r = OʻP = Distance of mid-point of small elementary portion CD from P.
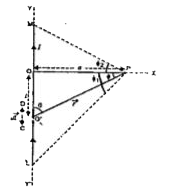
0 = Angle between the current carrying wire and the line joining the mid-point of CD to P, i.e., between →dl and →r .
According to Biot-Savart.s law, magnetic induction −→dB at the point P due to small current element CD is given by
−→dB=μ04πI→dl׈rr2
In magnitude dB=μ04πIdlsinθr2 ...(1)
and sinθ=dr=cosθ .....(2)
or r=acosϕ=asecϕ ....(3)
Also , tanϕ=l/aorl=atanϕ ....(4)
dl=asec2ϕdϕ
Substituting the values from eqns. (2), (3) and (4) in eqn. (1), we get
dB=μ04πI(asec2ϕdϕ)cosϕa2sec2ϕ
dB=μ0I4πacosϕdϕ ....(5)
Join PM and PL. Let ∠OPM.=ϕ2 and ∠OPL=−ϕ1
Then, magnetic field due to the whole length of conductor LM can be calculated by integrating eqn. (5) within the limits −ϕ1 to −ϕ2. Thus,
B=∫ϕ2−ϕ1dB=μ0I4πa∫ϕ2−ϕ1cosϕdϕ
=μ0I4πa[sinϕ]−θ2−θ1=μ0I4πa[sinϕ2−sin(ϕ1)]
=μ0I4πa[sinϕ2+sinϕ1] ....(6)
The above expression gives the magnitude of the magnetic field due to current carrying straight conductor of finite length.
If the conductor is infinitely long and the point P lies near the centre of the conductor, then
ϕ1=ϕ2=π2
So, B=μ0I4πa[sinπ2+sinπ2]
B=μ02I4πa
It is the expression for magnetic field due to an infinitely long current carrying straight conductor.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENTBOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - NUMERICALS PROBLEMS
3 Videos
- MAGNETIC EFFECTS OF CURRENTBOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - SHORT ANSWER TYPE QUESTIONS
4 Videos
- MAGNETIC DIPOLES AND EARTH'S MAGNETISMBOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC DIPOLES AND EARTH'S MAGNETISMEXERCISE - Most Expected Questions
8 Videos
- NUCLEAR REACTIONSBOOK - BETTER CHOICE PUBLICATIONCHAPTER - NUCLEAR REACTIONSEXERCISE - Numerical Problems
9 Videos
Similar Questions
A current of 15A flows through a coil Magnetic field at centre of semi-circular loop of 5.0 cm radius as shown in fig. Find out the direction and magnitude of magnetic field at the centre of the arc.

View SolutionExplain Biot-Savart law for the magnetic field produced at a point due to the current flowing in a current element. How will you determine the direction of the field?
View SolutionWhat do you mean by Neutral Point in a magnetic field?
View SolutionIt is given that each fission of a chain reaction produces 200 MeV energy. What is the number of fissions taking place per second it the reactor produces 1012W Power ?
View SolutionThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
View SolutionThe direction of magnetic field at a point due to an infinitely long wire carrying current is
View SolutionWrite the expression for magnetic flux at one end of a long solenoid carrying current.
View SolutionGive the expression for magnetic flux density at a point due to an infinitely long conductor perpendicular to it.
View SolutionGive the expression for magnetic flux density, at a point on the axis, due to a current carrying circular conductor.
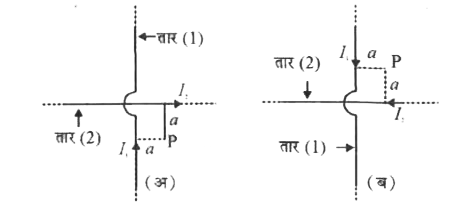
View Solutionचित्र में प्रदर्शित दो अनन्त लम्बाई के धारावाही चालक तारों के कारण बिंदु P पर परिणामी चुम्बकीय क्षेत्र ज्ञात कीजिए।
View SolutionUsing Ampere.s circuital law derive an expression for magnetic field due to infinitely long current carrying wire at a point at distance Yfrom it.
View SolutionDerive an expression for the magnetic field due to an infinitely long straight wire carrying current I.
View SolutionWrite the expression for the magnetic field produced by an infinitely straight wire carrying a current I at a short perpendicular distance a from itself.
View SolutionA famous law in physics is expressed as ointbarB.bar(dl)=mu_0I Using the above get an expression for the intensity of magnetic field at a point due to an infinite current carrying wire.
View Solutionएम्पियर का परिपथीय नियम लिखिये । इसे गणितीय रूप में व्यक्त कीजिये, इसके उपयोग से, अनन्त लम्बाई के, किसी धारा वाही चालक के कारण, चुम्बकीय क्षेत्र के मान के लिये एक व्यंजक प्राप्त कीजिये ।
View SolutionWrite expression for the magnetic flux density at a point due to a current carrying wire of: a finite length?
View Solution
