Question

Deduce the expression for the magnetic dipole moment of an electron orbitting around the central nucleus.

Explanation

Suppose an electron is revolving around the nucleus of an atom in anticlockwise direction. Let e= Charge on an electron
r= Radius of the orbit
`omega`= Angular velocity of electron
v= Orbital velocity of electron
`m_(e )` =Mass of electron
The orbital motion of electron constitutes current, which is given by `I= (e )/(T)`, where, T= Time in which electron completes one revolution.
`therefore I= (e )/((2pi)/(omega)) [because T= (2pi)/(omega)]`
or `I= (e omega)/(2pi)`...(i)
We know that magnetic moment of a current loop is given by M= IA
`M= I(pi r^(2))`, where `A= pi r^(2)`, area of loop.
Using eqn (i), we get `M = (e omega)/(2pi )(pi r^(2))`
or `M= (1)/(2) e omega r^(2)` ...(ii)
If the electron is supposed to be revolving in anticlockwise direction, then conventional current (I) flows in clockwise direction, therefore, upper face of the current loop behaves as S-pole while lower face as N-pole. The magnetic moment `(vec(M))` in this case acts perpendicular to the plane of atom and directed inward as shown in fig.
According to Bohr.s theory, the angular momentum `(vec(L))` of electron is an integral multiple of `(h)/(2pi)`, where h is Planck constant, i.e., `L= n h//2pi`...(iii)
where n is a natural number

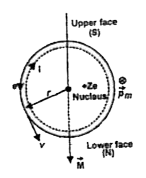
Also `L= m_(e) v r= m_(e) (r omega) r = m_(e) r^(2) omega` [`because` Linear velocity `=v = r omega`]
`therefore omega r^(2)= (L)/(m_(e ))= (n h)/(2pi m_(e ))` ...(iv)
From eqns (ii) and (iv)
`M= (1)/(2) e ((n h)/(2pi m_(e)))`
`M= (n e h)/(4pi m_(e))` ...(v)
It is clear from eqn (v) that value of the magnetic moment (M) will be least when n=1.
`therefore` Least value of magnetic moment is given by `M_(("least"))= (eh)/(4pi m_(e ))`
This least value of magnetic moment is known as Bohr.s mageton and denoted by `mu_(b)`.
`mu_(b)= (e h)/(4pi m_(e))`
Bohr.s Magneton: It is defined as the orbital magnetic moment of an electron revolving in the innermost orbit (n= I).