Question

Derive mirror formula for a convex mirror.

Explanation

For sign conventions, see Long Answer Type Question.No. 1
Let AS be an object placed on the-principal axis of a convex mirror as shown in Fig. The ray of light from point i?of the object travelling parallel to the principal axis falls at point Eon the mirror and is reflected along EQ, such that it appears to come from focus (F) of the convex mirror. Another ray of light incident at pole is reflected according to the laws of reflection along PQ.i.e.`angleBPA = angleQPA` . Also, the ray of light from point B incident on the mirror towards point C along BK will be reflected back and it will also appear to come from point B. The rays EQ, PQ and KB

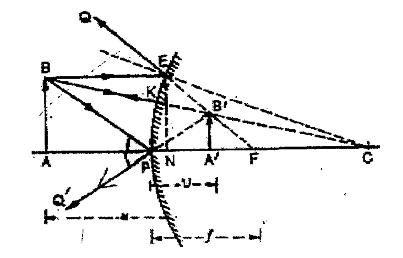
appear to come from point B. , so that the point B is image of the point B of the object. In the same manner, the image of every point on object AB will be produced at a corresponding point on AB, so that A.B is the virtual image of the object AB as formed by the convex mirror. From point E, drop EN perpendicular to the principal axis.
Now, triangles A.BF and ENFate similar. Therefore,
`(AB)/(NE) =(AF)/(NF)`
As aperture of the convex mirror is small, also, NF = PF and NE = AB
Therefore, `(AB)/(AB) = (AF)/(PF)`
Since, the distances are to be measured from pole of the mirror, we have . A.F= PF-PA.
`therefore (AB)/(AB) = (PF-PA)/(PF)`.....(i)
Also, triangles ABP and A.BPare similar. Therefore,
`(A.B.)/(AB) = (PA.)/(PA)`.........(ii)
From equations (i) and (ii), we have
`(PF - PA)/(PF) =(PA)/(PA)`..........(iii)
Applying sign conventions, we have:
`PA =+u`
`PA. = +v`
`PF =+f`
Substituting for PA, PA. and PF.m equation (iii), we have
`(+f -(+v))/(+f) = (+v)/(-u)` or `(f-v)/f = -v/u`
or `1-v/f =-u/v`
Divide throughout by v.
`1/v -1/f =-1/u`
or `1/u + 1/v = 1/f`
which is the required mirror formula.