Derive mirror equation for a convex mirror. Usingit, show that a convex mirror always produces a virtual image, independent of the location of object.

Text Solution

Verified by Experts

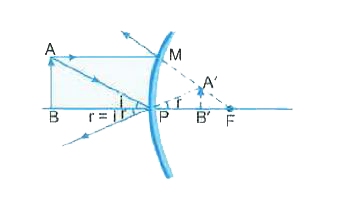
Let us consider image formation of a linear object AB placed in front of a convex mirror. As shown here a virtual, erect and diminished image A.B. is formed behind the mirror between its pole P and principal focus F.
Now $Δ A B P and Δ A . B . P$ are similar triangles and so.
$\frac{A . B .}{A B} = \frac{P B .}{P B} ....(i)$
Again as aperature of mirror is small MP may be taken as a straight line and then $Δ A . B . F$ and $Δ M P F$ are similar triangles. So,
$\frac{A . B .}{M D} = \frac{B . F}{P F}$
As MP = AB, we can write that $\frac{A . B .}{A B} = \frac{B . F}{P F} ...(ii)$
Comparing (i) and (ii), we get $\frac{P B .}{P B} = \frac{B . F}{P F}$
$\Rightarrow \frac{P B .}{P B} = \frac{P F - P B .}{P F}$
As per new Cartesian sign convention $P B = - u, P B . = + v e and P F = + f$ . So, we have
$\frac{(+ v e)}{(- u)} = \frac{(+ f) - (+ v)}{(+ f)} \Rightarrow v f = - u f + u v$
On dividing by uvf, we have
$\frac{1}{u} = - \frac{1}{v} + \frac{1}{f}$

$\Rightarrow \frac{1}{u} + \frac{1}{v} = \frac{1}{f}$ , which is the mirror formula.
As for a convex mirror f is $+ v e$ and u is $- v e$ , hence
$\frac{1}{v} = \frac{1}{f} - \frac{1}{(- u)} = \frac{1}{f} + \frac{1}{u}$
It means that $\frac{1}{v} > \frac{1}{u}$ or $| v | < | u |$
Thus, $m = \frac{h .}{h} = \frac{| v |}{∣ u} ∣ < 1$ i.e., the image is diminished one.
Moreover from above, it is clear that $\frac{1}{v} > \frac{1}{f} or | v | < | f |$
Hence, the image is located between the pole and principle focus of convex mirror.

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

An object placed at F of a convex mirror will produce an image
ABehind the mirror
BDiminished
CVirtual and erect
DAll of these

U-LIKE SERIES-CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)-SECTION D

Home
Ask Doubt
Profile