p+r+2q= 1 b. 2 c. 0 d. 4
To solve the equation p+r+2q=?, we need to analyze the given information and find the values of p, r, and q. However, the question does not provide explicit values or relationships for p, r, and q.
Let's assume we need to find the possible values of p+r+2q based on the options provided:
1. Identify the Variables: We have three variables: p, r, and q.
2. Analyze the Options: The options given are 1, 2, 0, and 4. We need to determine if any of these values can be expressed as p+r+2q.
3. Assume Values for Variables:
- Let's assume p=0, r=0, and q=0. Then:
p+r+2q=0+0+2(0)=0
- This gives us one possible solution, which matches option c (0).
4. Check Other Combinations:
- If we try p=1, r=0, and q=0:
p+r+2q=1+0+2(0)=1
- This matches option a (1).
- If we try p=2, r=0, and q=1:
p+r+2q=2+0+2(1)=4
- This matches option d (4).
5. Conclusion: Based on the combinations we tried, we found that p+r+2q can equal 0, 1, or 4. However, without further constraints or relationships between p, r, and q, we cannot definitively conclude which option is the only answer.
Thus, the possible values for p+r+2q can be 0, 1, or 4 based on the assumptions made.
2. Analyze the Options: The options given are 1, 2, 0, and 4. We need to determine if any of these values can be expressed as p+r+2q.
3. Assume Values for Variables:
- Let's assume p=0, r=0, and q=0. Then:
p+r+2q=0+0+2(0)=0
- This gives us one possible solution, which matches option c (0).
4. Check Other Combinations:
- If we try p=1, r=0, and q=0:
p+r+2q=1+0+2(0)=1
- This matches option a (1).
- If we try p=2, r=0, and q=1:
p+r+2q=2+0+2(1)=4
- This matches option d (4).
5. Conclusion: Based on the combinations we tried, we found that p+r+2q can equal 0, 1, or 4. However, without further constraints or relationships between p, r, and q, we cannot definitively conclude which option is the only answer.
Topper's Solved these Questions
Similar Questions
The equation [1xy][13402−1001]=[0] has fory=0 b. rational roots for y=−1 d. integral roots Then (ii) a. (p) (r) b. (q) (p) c. (p) (q) d. (r) (p)
View SolutionIf the difference of the roots of x2−px+q=0 is unity, then
a) p2+4q=1 b) p2−4q=1 c) p2+4q2=(1+2q)2 d) 4p2+q2=(1+2p)2
View SolutionSolution of dydx(x2y3+xy)=1 is , ey2p(1x+yr−q)=C Then
a. p=r
b. q+r=4
c. p+q+r=6
d. r=2
View SolutionIf a, b, c are pth, qth and rth terms of a GP, the |logap1logbq1logcr1| is equal to- log abc b. 1 c.0 d. pqr
View SolutionLet O(0,0),P(3,4), and Q(6,0) be the vertices of triangle OPQ . The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are a. (43,3) b. (3,23) c. (3,43) d. (43,23)
View SolutionIf p,q,r,s are rational numbers and the roots of f(x)=0 are eccentricities of a parabola and a rectangular hyperbola, where f(x)=px3+qx2+rx+s ,then p+q+r+s= a. p b. −p c. 2p d. 0
View SolutionMatch the columns and choose correct options.
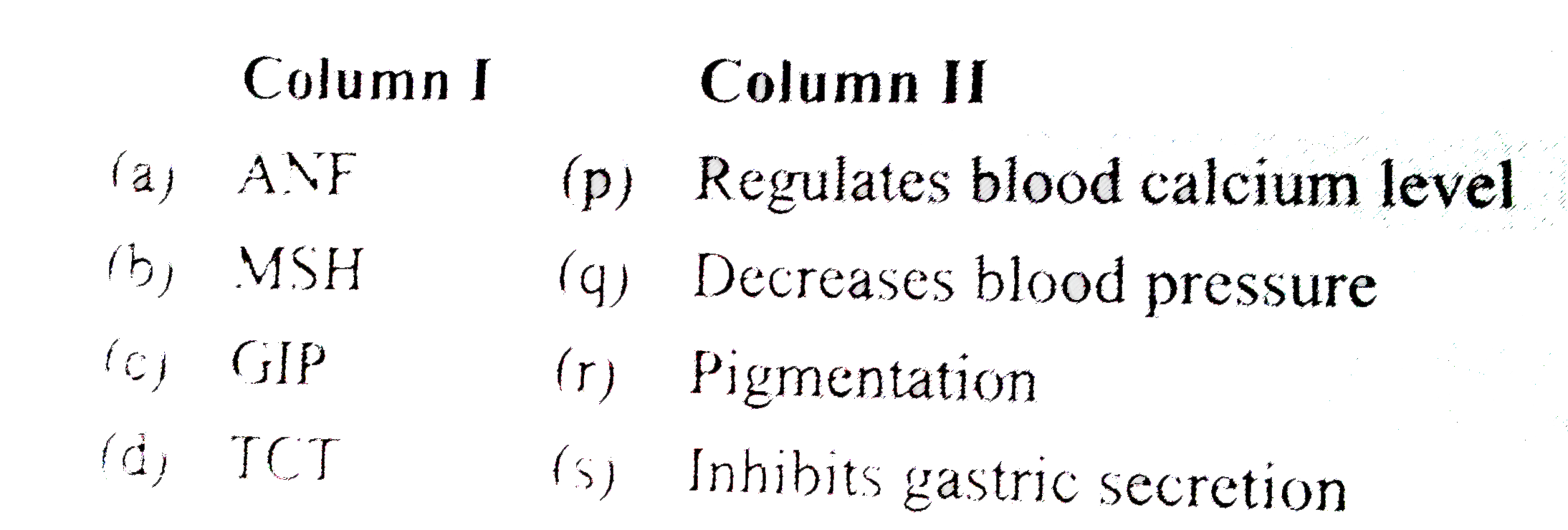
(1) a-q, b-r, c-s, d-p
(2) a-s, b-p, c-q, d-r
(3) a-q, b-p, c-s, d-r
(4) a-s, b-p, c-r, d-q
View SolutionGiven that q2−pr,0, p>0, then the value of |pqpx+qyqrqx+rypx+qyqx+ry0| is- a. zero b. positive c. negative d. q2+pr
View SolutionOf f(x)=px2+qx+r is a quadratic expression such that [a2a1b2b1c2c1][f(0)f(1)f(−1)]=[2a+12b+12c+1] for three unequal numbers a,b,c then p=32 (b) q=−12 (c) r=1 (d) p+q+r=2
View SolutionOf f(x)=px2+qx+r is a quadratic expression such that [a2a1b2b1c2c1][f(0)f(1)f(−1)]=[2a+12b+12c+1] for three unequal numbers a,b,c then (a) p=32 (b) q=−12 (c) r=1 (d) p+q+r=2
View Solution
