A fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
To solve the problem of finding the time taken by the water level to reach a height of H/2 from the bottom of a fixed container filled with water, we can follow these steps:
1. Understanding the Setup:
- We have a container of height H filled with water.
- There are two small orifices of cross-sectional area a: one at the bottom and another at a height of H/2 from the top (or H/2 from the bottom).
2. Defining Variables:
- Let h be the height of the water level at any time t.
- Initially, h=H when the container is full.
- We want to find the time t when h=H/2.
3. Applying Torricelli’s Law:
- The velocity of water flowing out of the bottom orifice (at height h) is given by:
V1=√2gh
- The velocity of water flowing out of the side orifice (which is at height H/2 from the top, or h−H/2 from the bottom) is:
V2=√2g(h−H/2)
4. Volume Flow Rate:
- The volume flow rate out of the bottom orifice is:
Q1=a⋅V1=a⋅√2gh
- The volume flow rate out of the side orifice is:
Q2=a⋅V2=a⋅√2g(h−H/2)
5. Rate of Change of Volume:
- The rate of decrease of volume in the container is equal to the sum of the volume flow rates out of the two orifices:
−Adhdt=Q1+Q2
- Thus, we have:
−Adhdt=a√2gh+a√2g(h−H/2)
6. Rearranging the Equation:
- Rearranging gives:
dhdt=−aA(√2gh+√2g(h−H/2))
7. Integrating to Find Time:
- To find the total time t for the height to decrease from H to H/2, we integrate:
t=−Aa√2g∫H/2Hdh√h+√h−H/2
8. Performing the Integration:
- The integration can be complex, but after performing it (using substitution or numerical methods), we find:
t=2a3√2g⋅H√H seconds
Final Result:
The time taken by the water level to reach a height of H/2 from the bottom of the container is:
t=2a3√2g⋅H1/2 seconds
- We have a container of height H filled with water.
- There are two small orifices of cross-sectional area a: one at the bottom and another at a height of H/2 from the top (or H/2 from the bottom).
- Let h be the height of the water level at any time t.
- Initially, h=H when the container is full.
- We want to find the time t when h=H/2.
- The velocity of water flowing out of the bottom orifice (at height h) is given by:
V1=√2gh
- The velocity of water flowing out of the side orifice (which is at height H/2 from the top, or h−H/2 from the bottom) is:
V2=√2g(h−H/2)
- The volume flow rate out of the bottom orifice is:
Q1=a⋅V1=a⋅√2gh
- The volume flow rate out of the side orifice is:
Q2=a⋅V2=a⋅√2g(h−H/2)
- The rate of decrease of volume in the container is equal to the sum of the volume flow rates out of the two orifices:
−Adhdt=Q1+Q2
- Thus, we have:
−Adhdt=a√2gh+a√2g(h−H/2)
- Rearranging gives:
dhdt=−aA(√2gh+√2g(h−H/2))
- To find the total time t for the height to decrease from H to H/2, we integrate:
t=−Aa√2g∫H/2Hdh√h+√h−H/2
- The integration can be complex, but after performing it (using substitution or numerical methods), we find:
t=2a3√2g⋅H√H seconds
The time taken by the water level to reach a height of H/2 from the bottom of the container is:
t=2a3√2g⋅H1/2 seconds
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)
16 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
Water rises to a height h in a capillary tube of cross-sectional area A. the height to which water will rise in a capillary tube of cross-sectional area 4A will be
View SolutionWater rises to a height h in a capillary tube of cross-sectional area A. the height to which water will rise in a capillary tube of cross-sectional area 4A will be
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
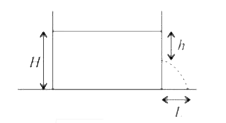
View SolutionA liquid is filled in a container to a height H. A small hole is opened in the side of the container a height h below the surface of the liquid. The distance L from the bottom of the container of the point where the stream of liquid leaving the container meets the ground is :
View SolutionA rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionA large tank filled with water to a height h is to be emptied through a small hole at the bottom. The ratio of times taken for the level of water to fall from h to h2 and from h2 to zero is
View SolutionIn a capillary tube having area of cross - section A, water rises to a height h. If cross-sectional area is reduced to A9, the rise of water in the capillary tube is
View SolutionOn the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
View SolutionA area of cross section of a large tank is 0.5m2. It has an opening near the bottom having area of cross section 1cm2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take g=10ms−2
View Solution