A vessel, whose bottom has round holes with diameter of 0.1 mm , is filled with water. The maximum height to which the water can be filled without leakage is (S.T. of water =75 dyne/cm , g=1000 cm/s)
100cm
75cm
50cm
30cm
The correct Answer is:D
To solve the problem of determining the maximum height to which water can be filled in a vessel with small holes at the bottom, we will use the concept of surface tension and hydrostatic pressure. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a vessel with holes at the bottom, and we need to find the maximum height (H) of water that can be filled without leaking through the holes. The diameter of the holes is given as 0.1 mm.
Step 2: Convert Units
First, we need to convert the diameter of the holes from millimeters to centimeters for consistency with the other units:
- Diameter (D) = 0.1 mm = 0.01 cm
- Radius (R) = D/2 = 0.01 cm / 2 = 0.005 cm
Step 3: Use the Formula for Capillary Rise
The height of the liquid column that can be supported by surface tension is given by the formula:
H=2⋅Tension⋅cos(θ)ρ⋅g⋅R
Where:
- Tension (Surface Tension) = 75 dyne/cm = 0.075 N/m (conversion to SI units)
- θ = angle of contact (for water, cos(0)=1)
- ρ = density of water = 1000 kg/m³ (which is 10³ g/cm³)
- g = acceleration due to gravity = 1000 cm/s² = 10 m/s² (conversion to SI units)
- R = radius in meters = 0.005 cm = 0.00005 m
Step 4: Substitute Values into the Formula
Now we can substitute the values into the formula:
H=2⋅0.075⋅11000⋅10⋅0.00005
Step 5: Calculate the Height
Calculating the denominator:
- 1000⋅10⋅0.00005=0.5
Now substituting this back into the equation:
H=2⋅0.0750.5=0.150.5=0.3 m
Step 6: Convert Height to Centimeters
To convert meters to centimeters:
H=0.3 m=30 cm
Final Answer
The maximum height to which the water can be filled without leakage is 30 cm.
---
We have a vessel with holes at the bottom, and we need to find the maximum height (H) of water that can be filled without leaking through the holes. The diameter of the holes is given as 0.1 mm.
First, we need to convert the diameter of the holes from millimeters to centimeters for consistency with the other units:
- Diameter (D) = 0.1 mm = 0.01 cm
- Radius (R) = D/2 = 0.01 cm / 2 = 0.005 cm
The height of the liquid column that can be supported by surface tension is given by the formula:
H=2⋅Tension⋅cos(θ)ρ⋅g⋅R
Where:
- Tension (Surface Tension) = 75 dyne/cm = 0.075 N/m (conversion to SI units)
- θ = angle of contact (for water, cos(0)=1)
- ρ = density of water = 1000 kg/m³ (which is 10³ g/cm³)
- g = acceleration due to gravity = 1000 cm/s² = 10 m/s² (conversion to SI units)
- R = radius in meters = 0.005 cm = 0.00005 m
Now we can substitute the values into the formula:
H=2⋅0.075⋅11000⋅10⋅0.00005
Calculating the denominator:
- 1000⋅10⋅0.00005=0.5
H=2⋅0.0750.5=0.150.5=0.3 m
To convert meters to centimeters:
H=0.3 m=30 cm
The maximum height to which the water can be filled without leakage is 30 cm.
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Fluid Statics)
40 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 2 (One or more than one correct answer)
53 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)
16 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A vessel whose , bottom has round holes with diameter 0.1mm, is filled with water. The maximum height up to which water can be filled without leakage is
View SolutionA vessel whose bottom has round holes with a diameter of d=0.1mm is filled with water. The maximum height of the water level h at which the water does not flow out, will be (The water does not wet the bottom of the vessel). [STofwater=70dyne/cm]
View Solution
Knowledge Check
A cylinder of height 20 m is completely filled with water. The velocity of efflux of water through a hole on the side wall of the cylinder near its bottom is (Take g=10ms−2)
A10ms−1B20ms−1C25.5 m s−1D5ms−1A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]A6B4C2D8
A vessel whose bottom has round holes with diameter of 1 mm is filled with water Assuming that surface tension acts only at holes, then the maximum height to which the water can be filled in vessel without leakage is (given surface tension of water is 75×10−3N/m) and g=10m/s2
View SolutionA container of height 10 cm is filled with water. There is hole at bottom. Find the pressure difference between point A & B .
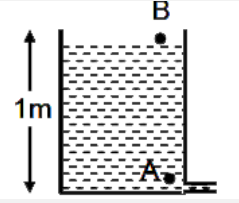
View SolutionA cylindrical beaker, whose base has a radius of 15 cm, is filled with water up to a height of 20 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the beaker. Find the increase in the level of water.
View SolutionA wide vessel with a small hole in the bottom is filled with water and kerosene. Find the velocity of water flow if the thickness of water layer is h1=30cm and that of kerosene is h2=20cm brgt

View SolutionA conical vessel of radius 6 cm and height 8 cm is completely filled with water. a sphere is lowered into the water and its size is such that when it touches the the sides, it just immersed. what fraction of water overflows.
View SolutionThere is a hole at the bottom of a large open vessel. If water is filled upto a height h, it flows out in time t. if water is filled to a height 4h, it will flow out in time
View Solution
