There is a hole at the bottom of a large open vessel. If water is filled upto a height h, it flows out in time t. if water is filled to a height 4h, it will flow out in time
t
4t
2t
t4
The correct Answer is:C
To solve the problem, we will use the principles of fluid dynamics and energy conservation. Here’s a step-by-step solution:
Step 1: Understand the problem
We have a large open vessel with a hole at the bottom. When the vessel is filled with water to a height h, it takes time t to empty. We need to find the time taken to empty the vessel when it is filled to a height 4h.
Step 2: Use Torricelli’s Law
According to Torricelli’s Law, the speed v of fluid flowing out of an orifice under the influence of gravity is given by:
v=√2gh
where h is the height of the water column above the hole.
Step 3: Calculate the time to empty the vessel for height h
When the water height is h, the speed of water flowing out is:
v=√2gh
The volume of water flowing out can be expressed in terms of the area of the hole A and the time t:
Volume=A⋅v⋅t
The volume of water in the vessel when filled to height h is:
Volume=A⋅h
Setting these equal gives:
A⋅h=A⋅v⋅t
Cancelling A from both sides (assuming A≠0):
h=v⋅t
Substituting v=√2gh:
h=√2gh⋅t
Step 4: Solve for time t
Rearranging gives:
t=h√2gh=h√2g⋅1√h=√h√2g
Step 5: Calculate the time to empty the vessel for height 4h
Now, when the height is 4h, the speed of water flowing out becomes:
v′=√2g(4h)=2√2gh
The volume of water when filled to height 4h is:
Volume=A⋅4h
Setting the volume equal to the outflow gives:
4h=v′⋅t′
Substituting v′:
4h=(2√2gh)⋅t′
Cancelling 2 from both sides:
2h=√2gh⋅t′
Solving for t′:
t′=2h√2gh=2⋅√h√2g=2t
Conclusion
Thus, the time taken to empty the vessel when filled to a height 4h is:
t′=2t
Final Answer
The time taken to empty the vessel when filled to a height 4h is 2t.
---
We have a large open vessel with a hole at the bottom. When the vessel is filled with water to a height h, it takes time t to empty. We need to find the time taken to empty the vessel when it is filled to a height 4h.
According to Torricelli’s Law, the speed v of fluid flowing out of an orifice under the influence of gravity is given by:
v=√2gh
where h is the height of the water column above the hole.
When the water height is h, the speed of water flowing out is:
v=√2gh
The volume of water flowing out can be expressed in terms of the area of the hole A and the time t:
Volume=A⋅v⋅t
The volume of water in the vessel when filled to height h is:
Volume=A⋅h
Setting these equal gives:
A⋅h=A⋅v⋅t
Cancelling A from both sides (assuming A≠0):
h=v⋅t
Substituting v=√2gh:
h=√2gh⋅t
Rearranging gives:
t=h√2gh=h√2g⋅1√h=√h√2g
Now, when the height is 4h, the speed of water flowing out becomes:
v′=√2g(4h)=2√2gh
The volume of water when filled to height 4h is:
Volume=A⋅4h
Setting the volume equal to the outflow gives:
4h=v′⋅t′
Substituting v′:
4h=(2√2gh)⋅t′
Cancelling 2 from both sides:
2h=√2gh⋅t′
Solving for t′:
t′=2h√2gh=2⋅√h√2g=2t
Thus, the time taken to empty the vessel when filled to a height 4h is:
t′=2t
The time taken to empty the vessel when filled to a height 4h is 2t.
Similar Questions
A hole is made at the bottom of a large vessel open at the top. If water is filled to a height h it drain out completely in time t. The time taken by the water column of height 4h to drain completely is
(a). √2t
(b). 2t
(c). 2√2t
(d). 4t
_S01_060_Q01.png)
View SolutionA cylindrical vessel is filled with water upto a height of 1m. The cross-sectional area of the orifice at the bottom is (1/400) that of the vessel.
(a) What is the time required to empty the tank through the orifice at the bottom?
(b) What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of 1m from orifice?
View Solution
Knowledge Check
A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]A6B4C2D8
There is a small hole in the bottom of a fixed container containing a liquid upto height 'h'. The top of the liquid as well as the hole at the bottom are exposed to atmosphere. As the liquid come out of the hole. (Area of the hole is 'a' and that of the top surface is 'A') :
View SolutionThe flat bottom of cylinder tank is silvered and water (μ=43) is filled in the tank upto a height h. A small bird is hovering at a height 3h from the bottom of the tank. When a small hole is opened near the bottom of the tank, the water level falls at the rate of 1 cm/s. The bird will perceive that his velocity of image is 1/x cm/sec (in downward directions) where x is
View SolutionA cylindrical tank of height H is open at the top end and it has a radius r. Water is filled in it up to a height of h. The time taken to empty the tank through a hole of radius r' in its bottom is
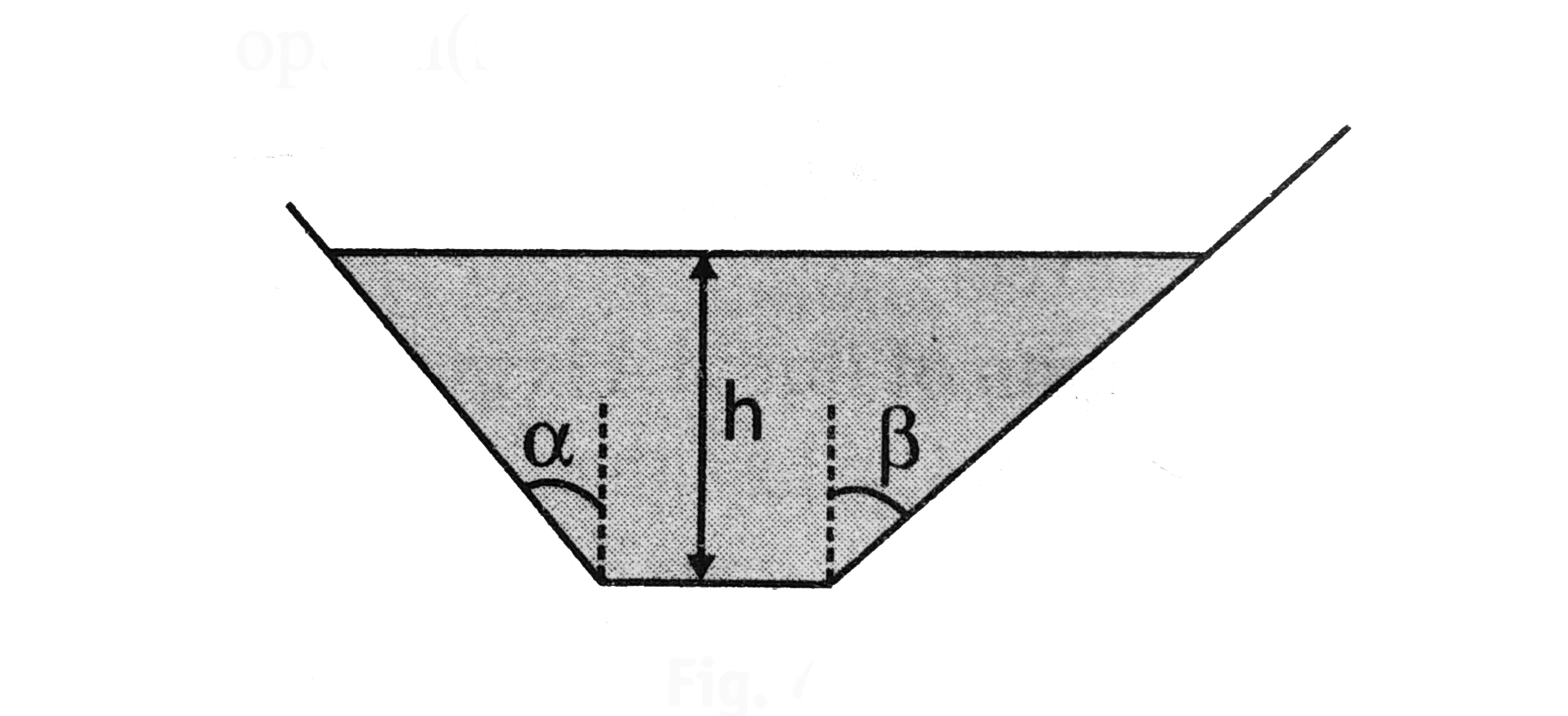
View SolutionA liquid is filled upto height h in a vessel, as shown. Find correct option(s):
View SolutionThere is a small hole at the bottom of tank filled with water. If total pressure at the bottom is 3atm(1atm=105Nm−2), then find the velocity of water flowing from hole.
View SolutionThere is a small hole at the bottom of tank filled with water. If total pressure at the bottom is 3atm(1atm=105Nm−2), then find the velocity of water flowing from hole.
View SolutionThere is a circular hole of diameter d=140μm at the bottom of a vessel containing mercury . The minimum height of mercury layer so that the mercury will not flow out of this hole is
( Surface tension, σ=490×10−3Nm−1)
View Solution
