When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Which of the following may be concluded from the information in the passage?
the volume flow rate and the mass flow rate are the more for more viscous fluids.
the volume flow rate is smaller for more viscous fluids whereas the mass flow rate is greater for more viscous fluids.
The volume flow rate is greater for more viscous fluids whereas the mass flow rate is smaller for more viscous fluids.
The volume flow rate and the mass flow rate are greater for less viscous fluids.
The correct Answer is:D
To solve the question based on the provided information, we will analyze the relationships between the volume flow rate, mass flow rate, and the coefficient of viscosity of fluids.
1. Understanding Viscous Force:
- According to Stokes' law, the viscous force Fw acting on a small sphere moving through a fluid is given by:
Fw=6πηrv
- Here, η is the coefficient of viscosity, r is the radius of the sphere, and v is the velocity of the sphere.
2. Volume Flow Rate:
- Poiseuille's law states that the volume flow rate Q through a pipe is given by:
Q=πR4(P2−P1)8ηL
- From this equation, we can see that the volume flow rate Q is inversely proportional to the coefficient of viscosity η. This means:
Q∝1η
- Therefore, as the viscosity increases, the volume flow rate decreases.
3. Mass Flow Rate:
- The mass flow rate ˙m can be related to the volume flow rate by the equation:
˙m=ρQ
- Since Q is inversely proportional to η, it follows that:
˙m∝1η
- This indicates that the mass flow rate also decreases as the viscosity increases.
4. Conclusion:
- Both the volume flow rate Q and the mass flow rate ˙m are inversely proportional to the coefficient of viscosity η. Therefore, for less viscous fluids (lower η), both the volume flow rate and mass flow rate will be higher.
5. Analyzing the Options:
- Based on the conclusions drawn:
- Option 1: Incorrect - states that both rates are more for more viscous fluids.
- Option 2: Incorrect - states volume flow rate is smaller for more viscous fluids but incorrectly claims mass flow rate is greater.
- Option 3: Incorrect - states volume flow rate is greater for more viscous fluids.
- Option 4: Correct - states that volume flow rate and mass flow rate are greater for less viscous fluids.
Final Answer:
The correct conclusion from the information in the passage is Option 4: Volume flow rate and mass flow rate are greater for less viscous fluids.
- According to Stokes' law, the viscous force Fw acting on a small sphere moving through a fluid is given by:
Fw=6πηrv
- Here, η is the coefficient of viscosity, r is the radius of the sphere, and v is the velocity of the sphere.
- Poiseuille's law states that the volume flow rate Q through a pipe is given by:
Q=πR4(P2−P1)8ηL
- From this equation, we can see that the volume flow rate Q is inversely proportional to the coefficient of viscosity η. This means:
Q∝1η
- Therefore, as the viscosity increases, the volume flow rate decreases.
- The mass flow rate ˙m can be related to the volume flow rate by the equation:
˙m=ρQ
- Since Q is inversely proportional to η, it follows that:
˙m∝1η
- This indicates that the mass flow rate also decreases as the viscosity increases.
- Both the volume flow rate Q and the mass flow rate ˙m are inversely proportional to the coefficient of viscosity η. Therefore, for less viscous fluids (lower η), both the volume flow rate and mass flow rate will be higher.
- Based on the conclusions drawn:
- Option 1: Incorrect - states that both rates are more for more viscous fluids.
- Option 2: Incorrect - states volume flow rate is smaller for more viscous fluids but incorrectly claims mass flow rate is greater.
- Option 3: Incorrect - states volume flow rate is greater for more viscous fluids.
- Option 4: Correct - states that volume flow rate and mass flow rate are greater for less viscous fluids.
The correct conclusion from the information in the passage is Option 4: Volume flow rate and mass flow rate are greater for less viscous fluids.
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Elasticity)
7 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Surface Tension)
5 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Assertion & Reason)
32 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
In the figure shown the straing versus stress graph for two values of young's modulus ?
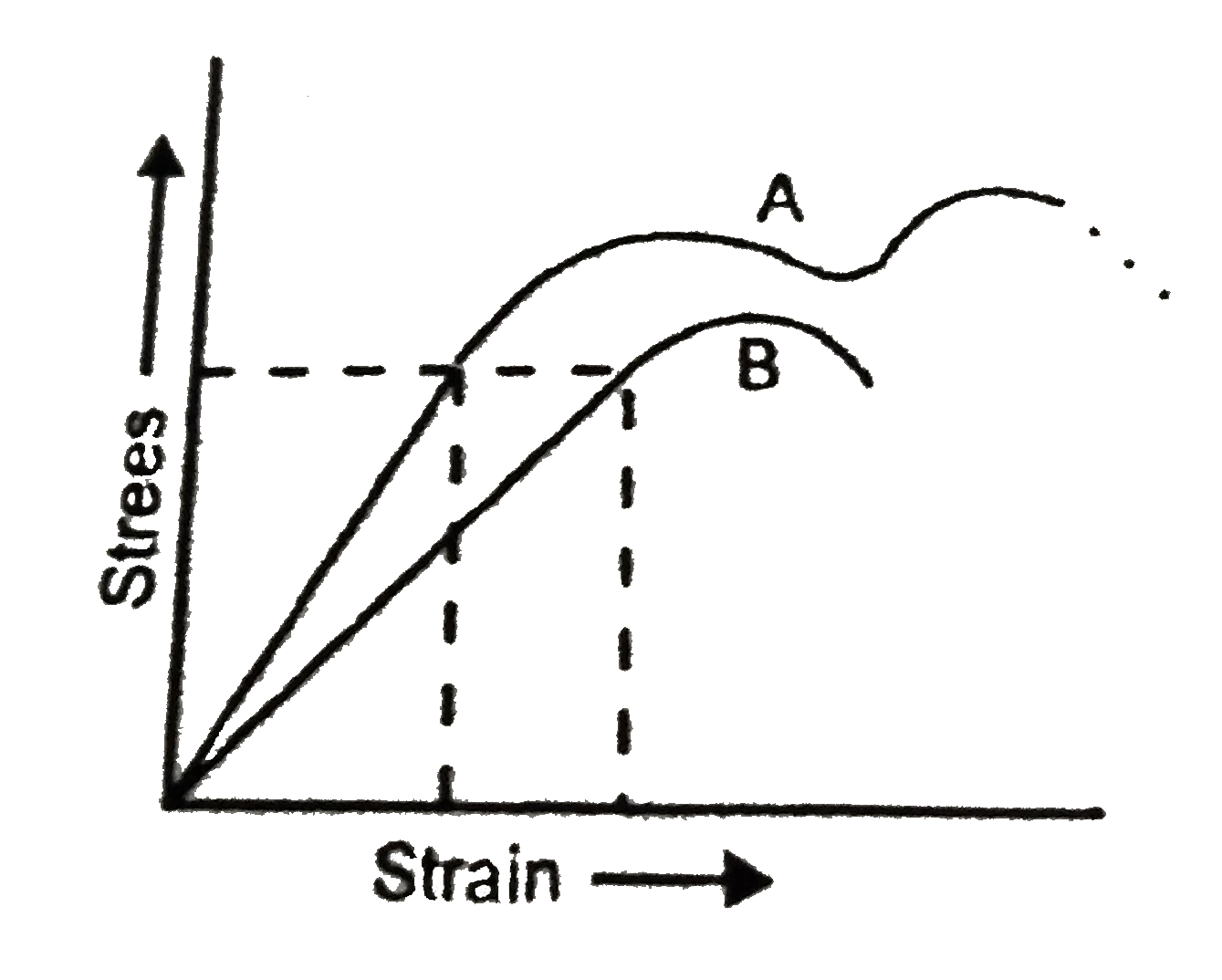
(i) which material is more ductile ? Explain.
(ii) Which material is more brittle ? Explain.
(iii) Which material is stronger ? Explain.
View Solution_E01_194_Q01.png)
PQRS is a rectangular frame of copper wire shown in figure the side RS of the frame is movable. If a soap film is formed on it then what is the diameter of the wire to maintain equilibirum (given surface tension of soap solution =0.045N/m and density of copper =8.96×103kg/m3)
View SolutionStatement-1: A solid sphere and a hollow sphere of same material and same radius are floating in a liquid. Same percentage of volume of both the spheres is immersed in the liquid.
Statement-2: Up-thrust force acts on volume of liquid displaced. It has nothing to do whether the body is solid or hollow.
View SolutionTwo particles of mases m1 and m2 in projectile motion have velocitie →v1 and →v2, respectively at time t=0. they collide at time t0. Their velocities become →v′1 and →v′2 at time 2t0 while still moving in air. The value of
∣∣(m1→v′1+m2→v′2)∣∣−|(m1→v1+m2→v2)| is
View SolutionA cube has a side of length 1.2×10−2m. Its volume upto correct significant figures is
View SolutionA sphere of mass M and radius R is falling in a viscous fluid. The terminal velocity attained by the falling object will be alphaortional to :
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Blood vessel is 0.10 m in length and has a radius of 1.5×10−2m blood flows at rate of 10−7m3/s through this vessel. The pressure difference that must be maintained in this flow between the two ends of the vessel is 20 Pa what is the viscosity sufficient of blood?
View SolutionA small metal sphere of radius a is falling with a velocity υ through a vertical column of a viscous liquid. If the coefficient of viscosity of the liquid is η, then the sphere encounters an opposing force of
View Solutionजब एक गोलाकार वस्तु किसी द्रव में चलती है तो द्रव उसपर गति की विपरीत दिशा में एक बल लगता है। इस बल का परिमाण F, द्रव का श्यानता गुणांक (coefficient of viscosity) η, गोले की त्रिज्या r तथा गोले के वेग v पर निर्भर करता है। विमाओं की सहायता से F के लिए η, v तथा r में सूत्र प्राप्त करे।
View SolutionViscous force on a small sphere of radius r moving in a fluid varies directly with
View SolutionA small metal sphere of radius a is falling with a velocity through a verticle column of a viscous liquid. If the coefficient of viscosity of the liquid is η, then the sphere encounters an opposing force of
View SolutionA small metal sphere of radius is rapidly falling down through a vertical viscous fluid column. The viscosity of this fluid eta This is the force that the metal sphere will feel against the motion
View SolutionA sphere of mass M and radius R is falling in a viscous fluid .The terminal velocity attained by the falling object will be proportional to ……
View SolutionA sphere of mass M and radius R is faling in a viscous fluid. The terminal velocity attained by the falling object will be proportional to
View SolutionA small metal sphere of radius a is falling with a velocity v through a vertical column of a viscous liquid. If the coefficient of viscosity of the liquid is eta , then the sphere encounters an opposing force of
View SolutionViscous force on a small sphere of radius r moving in a fluid varies directly with
View Solution
