A ship saslling from sea into a river sinks X mm and on discharging the corgo rises Y mm. on proceeding again into sea the ship rises the Zmm. Find te specific gravity of sea-water assuming the faces of ship are vertically along the line of sea water.
The correct Answer is:YY−X+Z
To solve the problem of finding the specific gravity of seawater given the conditions of the ship's movement between the sea and the river, we can follow these steps:
1. Understand the Forces Acting on the Ship:
- When the ship is floating, the weight of the ship (W_s) plus the weight of the cargo (W_c) is balanced by the buoyant force (B).
- The buoyant force is given by the formula:
B=density of fluid×volume submerged×g
- The volume submerged can be expressed as the area of the ship's base (A) multiplied by the height submerged (H_s).
2. Establish the Initial Condition in Seawater:
- Let the density of seawater be ρs. The equilibrium condition when the ship is in seawater can be expressed as:
Ws+Wc=ρs⋅A⋅Hs⋅g(Equation 1)
3. Condition When the Ship Moves into the River:
- When the ship moves from seawater to river water (density ρr), it sinks an additional X mm. Thus, the new submerged height is Hs+X.
- The equilibrium condition in the river becomes:
Ws+Wc=ρr⋅A⋅(Hs+X)⋅g(Equation 2)
4. Condition After Discharging Cargo:
- When the cargo is discharged, the ship rises by Y mm. The new submerged height is Hs+X−Y.
- The equilibrium condition after discharging the cargo in the river is:
Ws=ρr⋅A⋅(Hs+X−Y)⋅g(Equation 3)
5. Condition When the Ship Returns to the Sea:
- Upon returning to seawater, the ship rises by Z mm. The new submerged height is Hs+X−Y−Z.
- The equilibrium condition in seawater is:
Ws=ρs⋅A⋅(Hs+X−Y−Z)⋅g(Equation 4)
6. Subtracting Equations:
- Subtract Equation 2 from Equation 3 to eliminate Ws:
0=ρr⋅A⋅(Hs+X−Y)⋅g−ρr⋅A⋅(Hs+X)⋅g
- This simplifies to:
Wc=ρr⋅A⋅Y⋅g(Equation 5)
7. Using Equation 4:
- Substitute Equation 5 into Equation 4:
ρr⋅A⋅Y⋅g=ρs⋅A⋅(Hs+X−Y−Z)⋅g
- Cancel g and A:
ρr⋅Y=ρs⋅(Hs+X−Y−Z)
8. Finding Specific Gravity:
- Rearranging gives:
ρs=ρr⋅YHs+X−Y−Z
- The specific gravity of seawater is defined as:
Specific Gravity=ρsρr
- Substituting for ρs:
Specific Gravity=YY+Z−X
Final Answer:
The specific gravity of seawater is given by:
Specific Gravity=YY+Z−X
- When the ship is floating, the weight of the ship (W_s) plus the weight of the cargo (W_c) is balanced by the buoyant force (B).
- The buoyant force is given by the formula:
B=density of fluid×volume submerged×g
- The volume submerged can be expressed as the area of the ship's base (A) multiplied by the height submerged (H_s).
- Let the density of seawater be ρs. The equilibrium condition when the ship is in seawater can be expressed as:
Ws+Wc=ρs⋅A⋅Hs⋅g(Equation 1)
- When the ship moves from seawater to river water (density ρr), it sinks an additional X mm. Thus, the new submerged height is Hs+X.
- The equilibrium condition in the river becomes:
Ws+Wc=ρr⋅A⋅(Hs+X)⋅g(Equation 2)
- When the cargo is discharged, the ship rises by Y mm. The new submerged height is Hs+X−Y.
- The equilibrium condition after discharging the cargo in the river is:
Ws=ρr⋅A⋅(Hs+X−Y)⋅g(Equation 3)
- Upon returning to seawater, the ship rises by Z mm. The new submerged height is Hs+X−Y−Z.
- The equilibrium condition in seawater is:
Ws=ρs⋅A⋅(Hs+X−Y−Z)⋅g(Equation 4)
- Subtract Equation 2 from Equation 3 to eliminate Ws:
0=ρr⋅A⋅(Hs+X−Y)⋅g−ρr⋅A⋅(Hs+X)⋅g
- This simplifies to:
Wc=ρr⋅A⋅Y⋅g(Equation 5)
- Substitute Equation 5 into Equation 4:
ρr⋅A⋅Y⋅g=ρs⋅A⋅(Hs+X−Y−Z)⋅g
- Cancel g and A:
ρr⋅Y=ρs⋅(Hs+X−Y−Z)
- Rearranging gives:
ρs=ρr⋅YHs+X−Y−Z
- The specific gravity of seawater is defined as:
Specific Gravity=ρsρr
- Substituting for ρs:
Specific Gravity=YY+Z−X
The specific gravity of seawater is given by:
Specific Gravity=YY+Z−X
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 A (Previous year Questions)
29 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (MCQ)
13 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Viscosity)
3 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
Why can a ship not use the internal energy of sea water to operate its engine?
View SolutionWhen a ship enters sea water from fresh water it sinks less.
View SolutionA loaded cargo ship sails from sea water to river water? State and explain your observation.
View SolutionWhy is it impossible for a ship to use the internal energy of sea water to operate its engine?
View SolutionTwo ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships are observed from the top of the light house are 60∘ and 45∘ respectively. If the height of the light house is 200 m, find the distance between the two ships. (Use √3=1.73)
View SolutionExplain the following:
A ship submerges more as it sails from sea water to river water.
View SolutionA ship is salling in river. An observe is situated at a depth h in water (μw). If x>>h, find the angle made form vertical, of the line of slight of ship.

View Solution‘Skysails’ is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The ‘Skysails’ technology allows the towing kite to gain a height of anything between 100 metres – 300 metres.The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a ‘telescopic mast’ that enables the kite to be raised properly and effectively.
Based on the following figure related to sky sailing, answer the questions
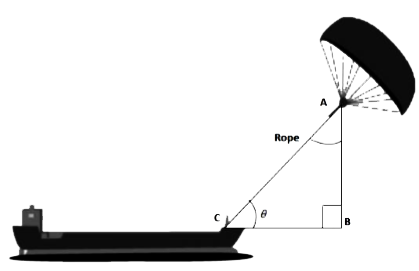
(i) In the given figure, if sinθ=cos(3θ−30∘), where θ and 3θ−30∘ are acuts angle, then find the value of θ.
(ii) What should be the length of the rope of the kite sail in order to pull the ship at the angle θ (calculated above) and be at a vertical height of 200 m?
View SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
If the velocity profile is given by
v=23y−y2v is velocity in m/secy is in meter above the bad. Determine shear stress at y=0.15m, & η=0.863Ns/m2
View SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
Viscosity of liquids
View Solution
