A ship is salling in river. An observe is situated at a depth h in water (μw). If x>>h, find the angle made form vertical, of the line of slight of ship.
C=sin−1(μaμw)
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1141videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-262videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS16videos
GRAVITATION
Similar Questions
A rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
View SolutionA small wooden rod of length 5mm is fixed at the bottom of the container filled with water (μwater=43). It is making an angle 37∘ with vertical. If an observer (in air) observes the rod paraxially, and the rod is appearing at an angle πx radian with vertical then the find the value of x.
View SolutionTwo ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships are observed from the top of the light house are 60∘ and 45∘ respectively. If the height of the light house is 200 m, find the distance between the two ships. (Use √3=1.73)
View SolutionA ship saslling from sea into a river sinks X mm and on discharging the corgo rises Y mm. on proceeding again into sea the ship rises the Zmm. Find te specific gravity of sea-water assuming the faces of ship are vertically along the line of sea water.
View SolutionA man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60∘ and the angle of depression the base of hill as 30∘. Find the distance of the hill from the ship and the height of the hill.
View SolutionFrom the top of a light house, the angles of depression of two ships on the opposite sides of its are observed to be αandβ . If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is htanα+tanβtanαtanβ
View SolutionA stationary observer O looking at a fish F in water (μw=4/3) through a converging lens of focal length 90.0cm . The lens is allowed to fall frelly from a height 62.0cm with its axis vertical. The fish and the observer are on the principal axis of the lens. The fish moves up with constant velocity 100cm/s. Initially it was at depth of 44.0cm . Find the velocity (in cm//s) with which the fish appears to move with respect to lens to the observer at t=0.2s. (take g=10m/s2)
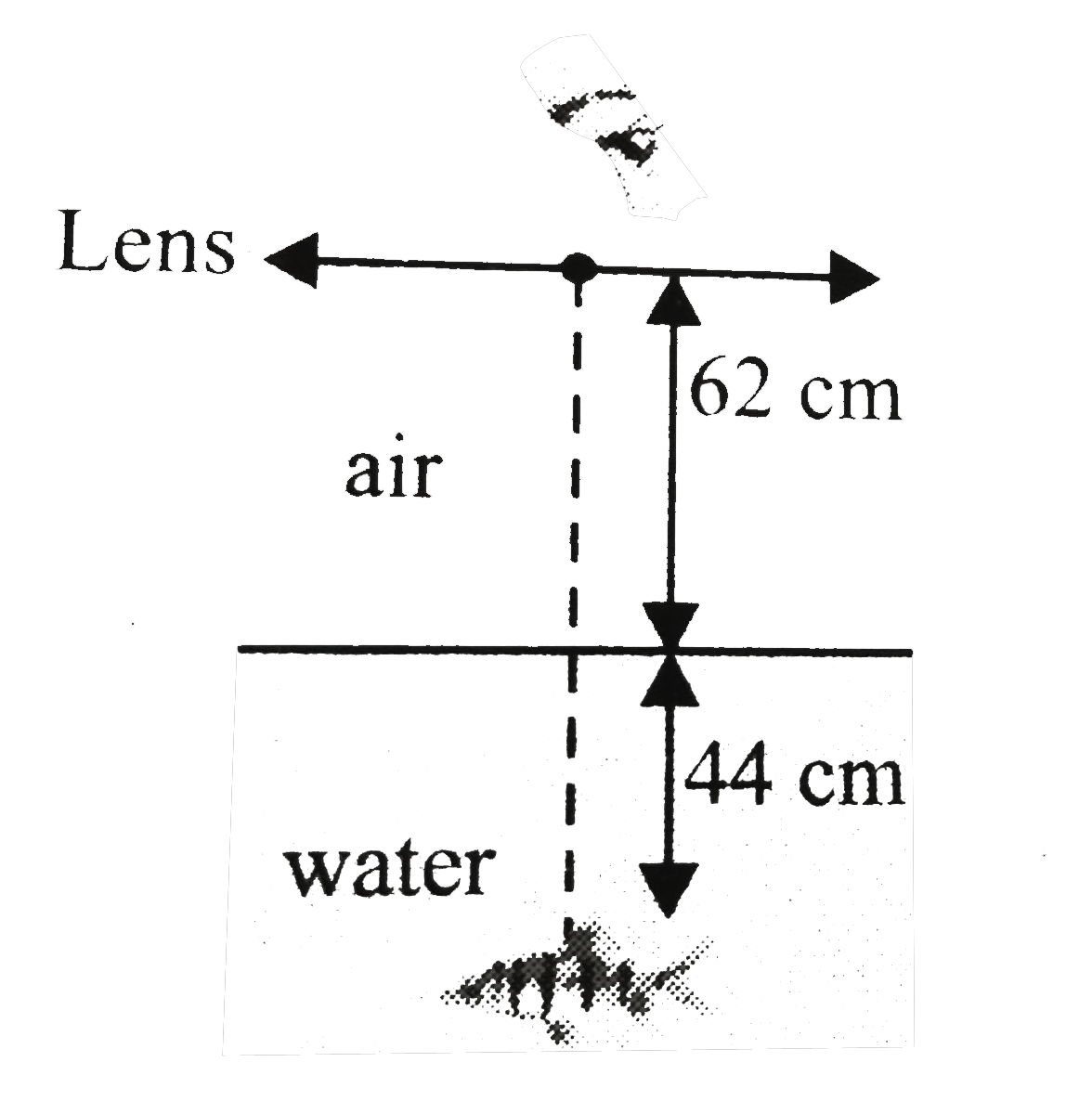View SolutionA jet of water is projected at an angle θ=45∘ with horizontal from point A which is situated at a distance x=OA=(a)1/2m,(b)2m from a vertical wall. If the speed of projection is v0=√10ms−1, find point P of strinking of the water jet with the vertical wall.
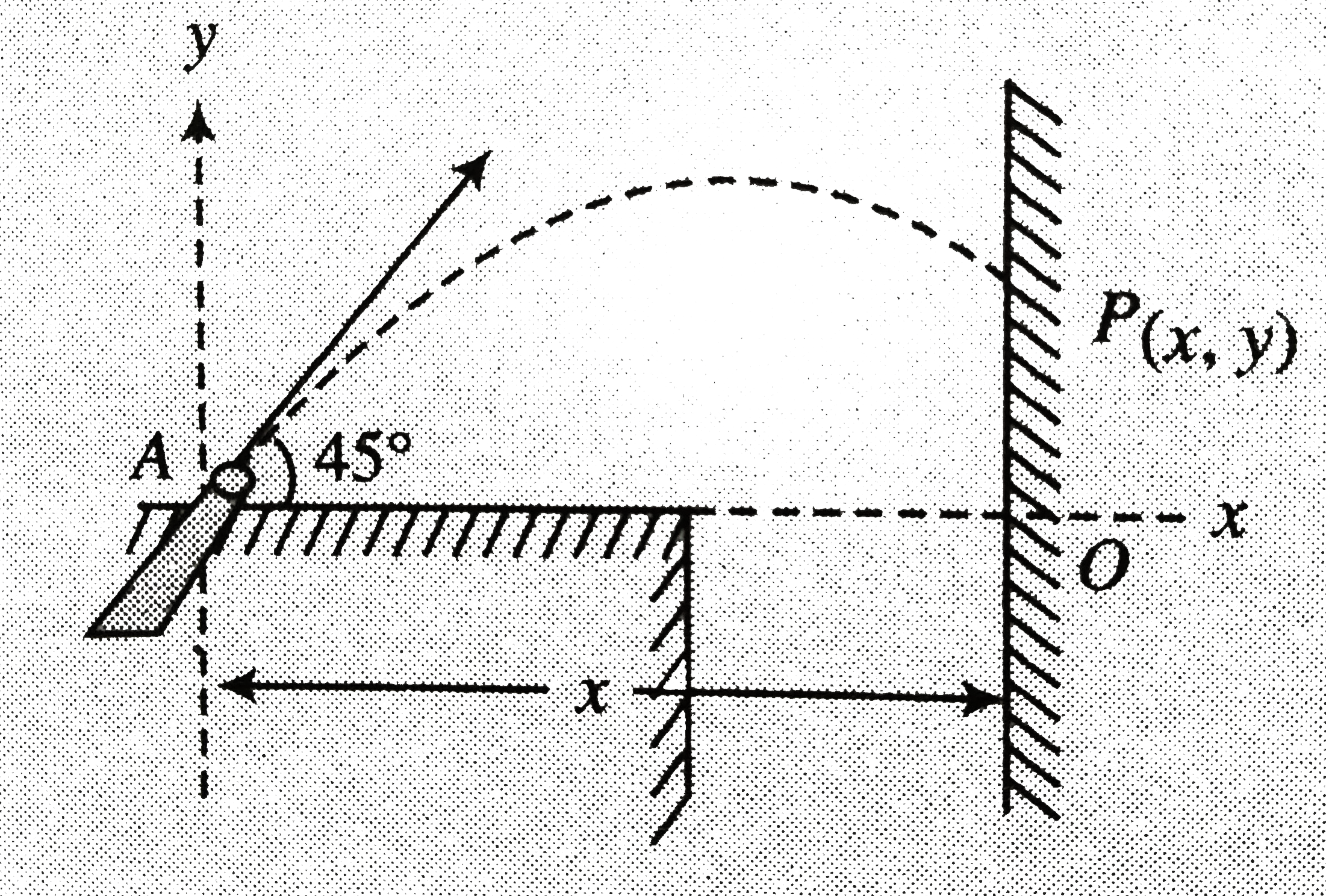.View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a) Find the total force exerted by the water on the bottom surface of the tank. b) Consider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water.Find the force by the water on this strip. c) Find the torque of the force calculate in part b) about the bottom edge of this side. d) Find the total force by the water on this side. e) Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View SolutionFrom the top of a light-hours, the angles of depression of two ships on the opposite sides are observed to be 30∘ and 45∘. If the height of the light-house, is 90 m and the line joining the two ships passes through the light- house, then find the distance between the ships.
View Solution