Find the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.
The correct Answer is:−GMmlloge(1+la)
To solve the problem of finding the gravitational potential energy of a point mass m and a thin uniform rod of mass M and length l, we will follow these steps:
Step 1: Set up the problem
We have a thin uniform rod of mass M and length l. The point mass m is located at a distance a from one end of the rod. We can denote the position of the point mass and the rod in a coordinate system.
Step 2: Define the small mass element
Consider a small element of the rod of length dx at a distance x from the point mass m. The mass of this small element can be expressed as:
dm=Mldx
where Ml is the mass per unit length of the rod.
Step 3: Write the expression for potential energy
The gravitational potential energy dU between the point mass m and the small mass element dm is given by:
dU=−Gmdmx
Substituting for dm:
dU=−Gmx⋅Mldx
Step 4: Determine the limits of integration
The limits of integration for x will be from a (the position of the point mass) to a+l (the far end of the rod).
Step 5: Integrate to find total potential energy
Now we can integrate dU to find the total potential energy U:
U=−GmMl∫a+la1xdx
The integral of 1x is lnx:
U=−GmMl(lnx)a+la
Evaluating the limits:
U=−GmMl(ln(a+l)−ln(a))
Using the property of logarithms:
U=−GmMlln(a+la)
Step 6: Find the force of interaction
The force F of their interaction can be found by taking the derivative of the potential energy U with respect to a:
F=−dUda
Calculating the derivative:
F=−GmMl⋅1a+la⋅dda(a+la)
Using the quotient rule:
F=−GmMl⋅(1a−1a+l)
Simplifying:
F=−GmMl⋅((a+l)−aa(a+l))=−GmMl⋅la(a+l)
Thus, the force of interaction is:
F=−GmMa(a+l)
Final Results
1. The potential energy U of the gravitational interaction is:
U=−GmMlln(a+la)
2. The force of interaction F is:
F=−GmMa(a+l)
We have a thin uniform rod of mass M and length l. The point mass m is located at a distance a from one end of the rod. We can denote the position of the point mass and the rod in a coordinate system.
Consider a small element of the rod of length dx at a distance x from the point mass m. The mass of this small element can be expressed as:
dm=Mldx
where Ml is the mass per unit length of the rod.
The gravitational potential energy dU between the point mass m and the small mass element dm is given by:
dU=−Gmdmx
Substituting for dm:
dU=−Gmx⋅Mldx
The limits of integration for x will be from a (the position of the point mass) to a+l (the far end of the rod).
Now we can integrate dU to find the total potential energy U:
U=−GmMl∫a+la1xdx
The integral of 1x is lnx:
U=−GmMl(lnx)a+la
Evaluating the limits:
U=−GmMl(ln(a+l)−ln(a))
Using the property of logarithms:
U=−GmMlln(a+la)
The force F of their interaction can be found by taking the derivative of the potential energy U with respect to a:
F=−dUda
Calculating the derivative:
F=−GmMl⋅1a+la⋅dda(a+la)
Using the quotient rule:
F=−GmMl⋅(1a−1a+l)
Simplifying:
F=−GmMl⋅((a+l)−aa(a+l))=−GmMl⋅la(a+l)
Thus, the force of interaction is:
F=−GmMa(a+l)
1. The potential energy U of the gravitational interaction is:
U=−GmMlln(a+la)
2. The force of interaction F is:
F=−GmMa(a+l)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 4 B (Brain Storming Subjective Exercise)20videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 5 A (Previous Year Questions)26videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)20videos
GRAVITATION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)46videos
KINEMATICS-2D
Similar Questions
Find the potential V at P in the gravitational field of fixed point mass M.
View SolutionFind aC and α of the smooth rod of mass m and length l.
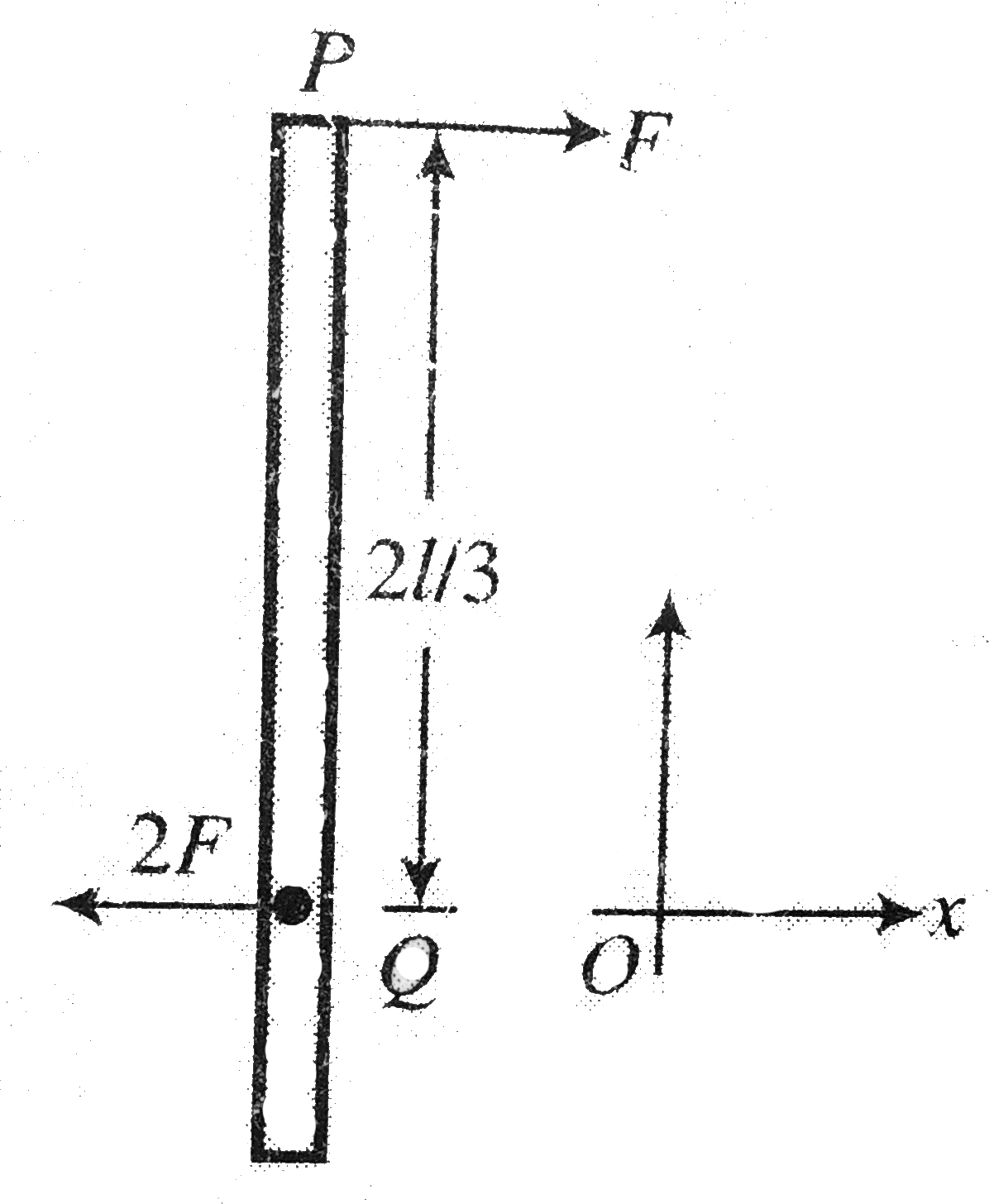 View Solution
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionCalculate the self-gravitational potential energy of matter forming a. a thin uniform shell of mass M and radius R, b. a uniform sphere of mass m and radius R.
View SolutionA rod of mass M and length L is made to stand vertically. Potential energy of the rod in this position is
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as
 View Solution
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View Solution

