A detector at x=0 receives waves from three sources each of amplitude A and frequencies f+2,f and f−2.
The time at which intensity is maximum, is
t=0,1/4,1/2,3/4,…sec
t=1/6,1/3,2/3,5/6,…sec
t=0,1/2,3/2,5/2,..sec
t=1/2,1/4,1/6,1/8,…sec
The correct Answer is:A
To find the time at which the intensity is maximum at the detector located at x=0, we can follow these steps:
Step 1: Understand the wave sources
We have three sources emitting waves with the following frequencies:
- Source 1: f+2
- Source 2: f
- Source 3: f−2
Step 2: Write the wave equations
The wave equations for the three sources can be expressed as:
- y1(t)=Asin(2π(f+2)t)
- y2(t)=Asin(2πft)
- y3(t)=Asin(2π(f−2)t)
Step 3: Combine the waves
The total wave at the detector is the sum of the individual waves:
y(t)=y1(t)+y2(t)+y3(t)
This can be simplified using the sine addition formula.
Step 4: Find the resultant frequency
The frequencies of the waves are f+2, f, and f−2. The maximum frequency difference is 4 (from f+2 to f−2). The resultant frequency of the combined wave will be the average of these frequencies:
favg=f
The beat frequency will be 4 (the difference between the highest and lowest frequencies).
Step 5: Determine the condition for maximum intensity
The intensity of the resultant wave is maximum when the phase difference between the waves is an integer multiple of 2π. This occurs when:
sin(4πt)=0
This means:
4πt=nπ(n is an integer)
Thus:
t=n4
Step 6: Identify specific times
The times at which the intensity is maximum are:
- t=0
- t=14
- t=12
- t=34
- and so on...
Conclusion
The times at which the intensity is maximum are given by:
t=n4(n=0,1,2,3,…)
We have three sources emitting waves with the following frequencies:
- Source 1: f+2
- Source 2: f
- Source 3: f−2
The wave equations for the three sources can be expressed as:
- y1(t)=Asin(2π(f+2)t)
- y2(t)=Asin(2πft)
- y3(t)=Asin(2π(f−2)t)
The total wave at the detector is the sum of the individual waves:
y(t)=y1(t)+y2(t)+y3(t)
This can be simplified using the sine addition formula.
The frequencies of the waves are f+2, f, and f−2. The maximum frequency difference is 4 (from f+2 to f−2). The resultant frequency of the combined wave will be the average of these frequencies:
favg=f
The beat frequency will be 4 (the difference between the highest and lowest frequencies).
The intensity of the resultant wave is maximum when the phase difference between the waves is an integer multiple of 2π. This occurs when:
sin(4πt)=0
This means:
4πt=nπ(n is an integer)
Thus:
t=n4
The times at which the intensity is maximum are:
- t=0
- t=14
- t=12
- t=34
- and so on...
The times at which the intensity is maximum are given by:
t=n4(n=0,1,2,3,…)
Topper's Solved these Questions
Similar Questions
A detector at x=0 receives waves from three sources each of amplitude A and frequencies f+2,f and f−2.
If I0∝A2, then the value of maximum intensity,isView SolutionA detector at x=0 receives waves from three sources each of amplitude A and frequencies f+2,f and f−2.
The equation of waves are : y1=Asin[2π(f+2),y2=Asin2πft and y3=Asin[2π(f−2)t]. The time at which intensity is minimum isView Solution
Knowledge Check
- Question 1 - Select One
Two sounds A and B are of same amplitudes, same wave forms but of frequencies f and 2f respectively. Then :
AB differ in quality from ABB is grave, A is shrillCB is shrill, A is graveDB is louder than A.
Y=2Acos2(kx−ωt) represents a wave with amplitude A´ and frequency f. The value of A´ and f are:
View SolutionA detector is released from rest over a source of sound of frequency f0=103Hz. The frequency observed by the detector at time t is plotted in the graph. The speed of sound in air is (g=10m/s2)
 View Solution
View SolutionWhen two sound waves with a phase difference of π/2, and each having amplitude A and frequency ω , are superimposed on each other, then the maximum amplitude and frequency of resultant wave is
View Solution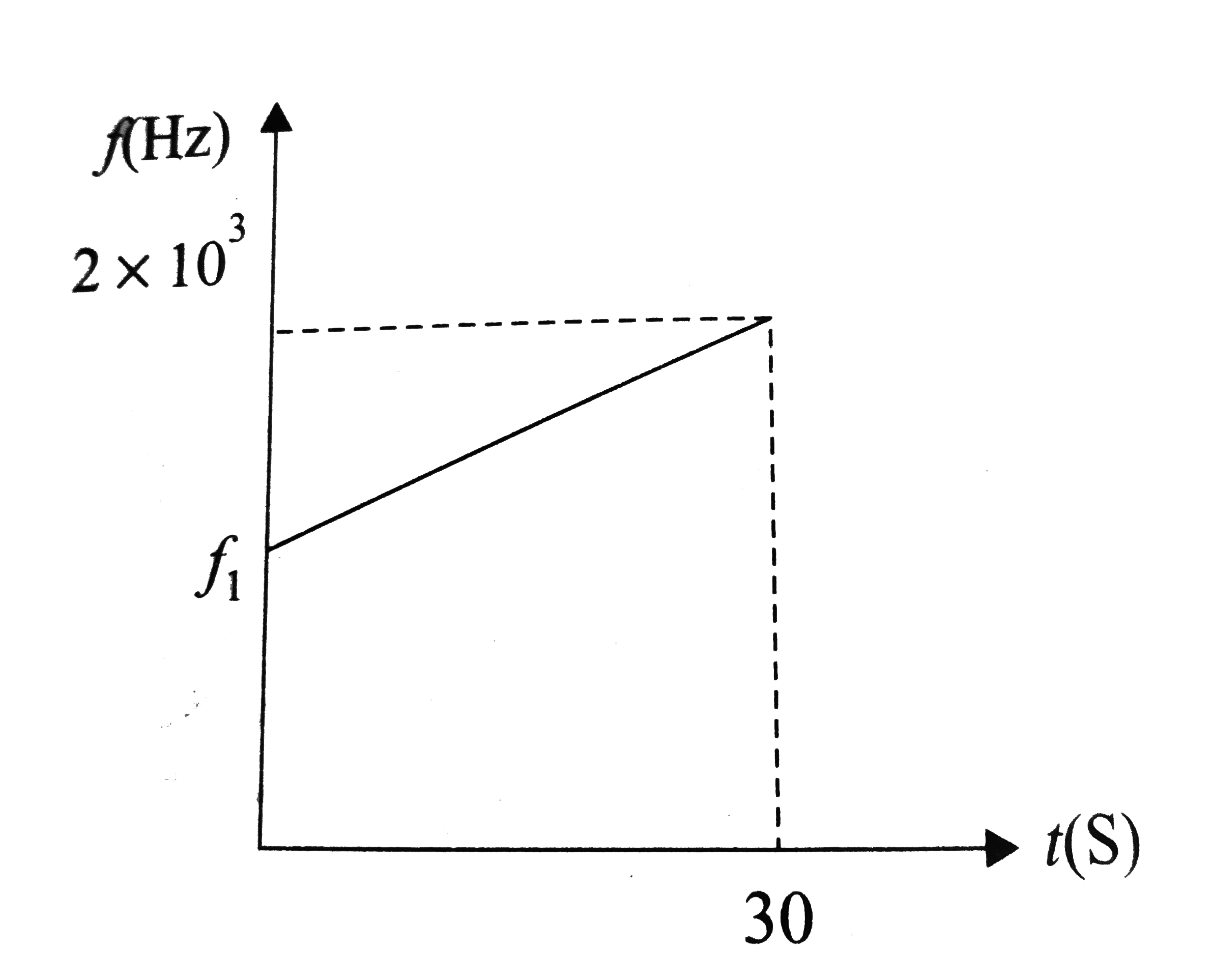
A source of sound of frequency f1 is placed on the ground. A detector placed at a height is released from rest on this source. The observed frequency f(Hz) is plotted against time t(sec) . The speed of sound in air is 300ms. Find f1 (g=10ms).View Solution
A source of sound of frequency f1 is placed on the ground. A detector placed at a height is released from rest on this source. The observed frequency f(Hz) is plotted against time t(sec) . The speed of sound in air is 300ms. Find f1 (g=10ms).View Solution
A source of sound of frequency f1 is placed on the ground. A detector placed at a height is released from rest on this source. The observed frequency f(Hz) is plotted against time t(sec) . The speed of sound in air is 300ms. Find f1 (g=10ms).View SolutionA source of sound is moving along a circular orbit of radius 3meter with an angular velocity of 10rad/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with an amplitude BC=CD=6meters. The frequency of oscillation of the detector is 5π per second. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340Hz, Find the maximum and the minimum frequencies recorded by the detector.
 View Solution
View Solution

