Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air=320ms−1
The correct Answer is:1200Hz,2000Hz,2800Hz,3600Hz,4400Hz
To solve the problem of finding the frequencies for which there is destructive interference at the listener's position, we will follow these steps:
Step 1: Determine the Path Difference
The listener is located 6.0 m from speaker S1 and 6.4 m from speaker S2. The path difference (Δd) can be calculated as:
Δd=d2−d1=6.4m−6.0m=0.4m
Step 2: Condition for Destructive Interference
For destructive interference to occur, the path difference must be an odd multiple of half the wavelength (λ):
Δd=(2n+1)λ2
where n is an integer (0, 1, 2, ...).
Step 3: Express Wavelength in Terms of Frequency
The wavelength (λ) can be expressed using the speed of sound (v) and frequency (f):
λ=vf
Given that the speed of sound in air is v=320m/s, we can substitute this into the equation for path difference:
0.4=(2n+1)v2f
Substituting v:
0.4=(2n+1)3202f
This simplifies to:
0.4=(2n+1)160f
Step 4: Rearranging to Find Frequency
Rearranging the equation to solve for frequency f:
f=(2n+1)⋅400
Step 5: Finding Frequencies within the Given Range
We need to find the values of f for n=0,1,2,... that lie within the range of 500 Hz to 5000 Hz.
1. For n=0:
f=(2⋅0+1)⋅400=400Hz(not in range)
2. For n=1:
f=(2⋅1+1)⋅400=1200Hz(in range)
3. For n=2:
f=(2⋅2+1)⋅400=2800Hz(in range)
4. For n=3:
f=(2⋅3+1)⋅400=3600Hz(in range)
5. For n=4:
f=(2⋅4+1)⋅400=4400Hz(in range)
6. For n=5:
f=(2⋅5+1)⋅400=5200Hz(not in range)
Conclusion
The frequencies for which there is destructive interference at the listener's position are:
- 1200 Hz
- 2800 Hz
- 3600 Hz
- 4400 Hz
The listener is located 6.0 m from speaker S1 and 6.4 m from speaker S2. The path difference (Δd) can be calculated as:
Δd=d2−d1=6.4m−6.0m=0.4m
For destructive interference to occur, the path difference must be an odd multiple of half the wavelength (λ):
Δd=(2n+1)λ2
where n is an integer (0, 1, 2, ...).
The wavelength (λ) can be expressed using the speed of sound (v) and frequency (f):
λ=vf
Given that the speed of sound in air is v=320m/s, we can substitute this into the equation for path difference:
0.4=(2n+1)v2f
Substituting v:
0.4=(2n+1)3202f
This simplifies to:
0.4=(2n+1)160f
Rearranging the equation to solve for frequency f:
f=(2n+1)⋅400
We need to find the values of f for n=0,1,2,... that lie within the range of 500 Hz to 5000 Hz.
f=(2⋅0+1)⋅400=400Hz(not in range)
f=(2⋅1+1)⋅400=1200Hz(in range)
f=(2⋅2+1)⋅400=2800Hz(in range)
f=(2⋅3+1)⋅400=3600Hz(in range)
f=(2⋅4+1)⋅400=4400Hz(in range)
f=(2⋅5+1)⋅400=5200Hz(not in range)
The frequencies for which there is destructive interference at the listener's position are:
- 1200 Hz
- 2800 Hz
- 3600 Hz
- 4400 Hz
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[B]
13 Videos
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[A]
28 Videos
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-03)
31 Videos
- SEMICONDUCTORSBOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
51 Videos
Similar Questions
The frequency of the whistle of a train is observed to drop from 280 Hz to 260 Hz as the train moves away from a stationary listerner on the platform. Calculate the speed of the train, if speed of sound in air is 340 m/s.
View SolutionFigure 7.20 shows a tube structure in which signal is sent from one end and is received at the other end . The frequency of the sound source can be varied electronically between 2000→5000Hz. Find the frequencies at which maxima of intensity are detected . The speed of sound in air 340m/s.

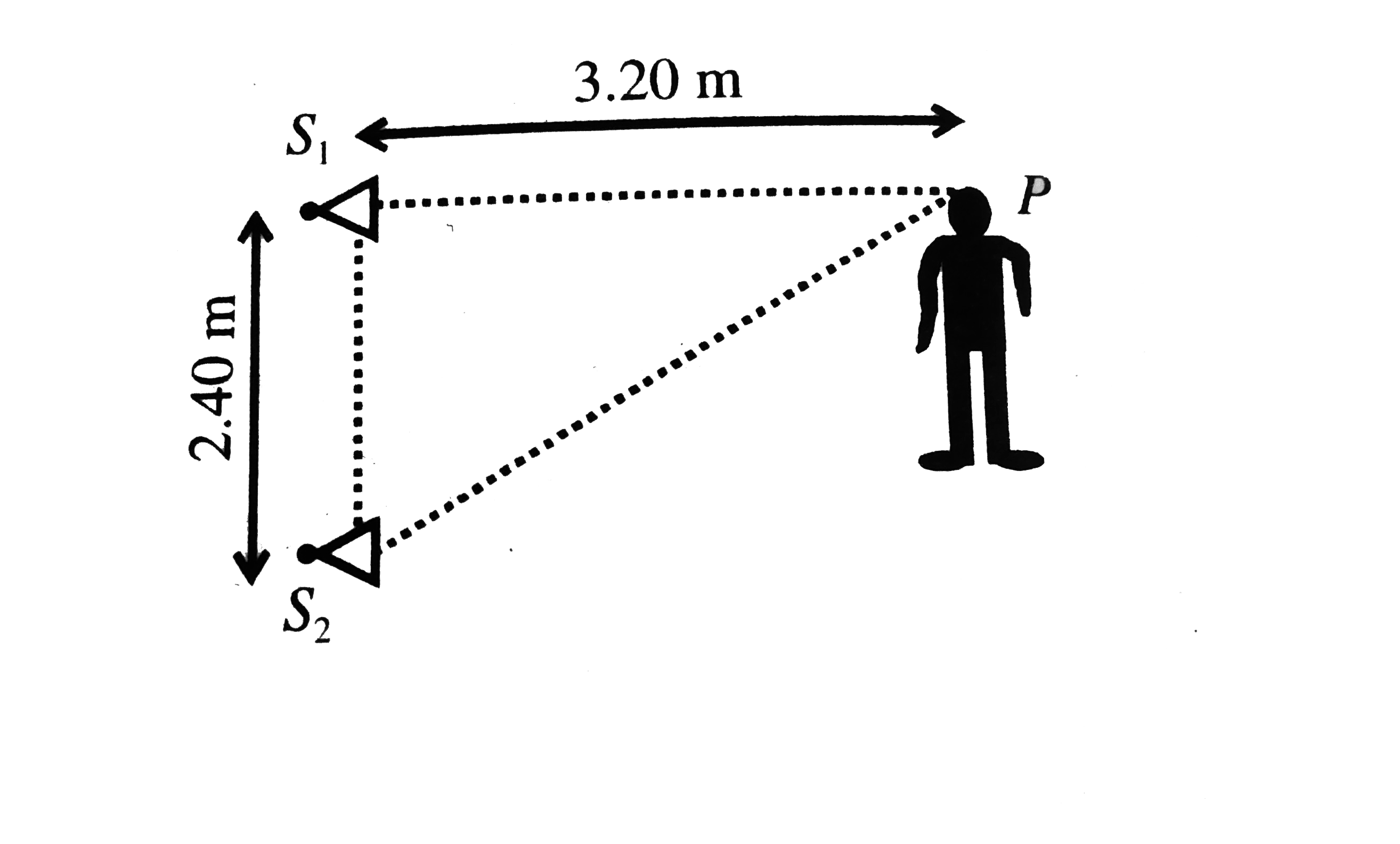
View SolutionTwo stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1

View SolutionTwo stereo speaks S1andS2 are separated by a distance of 2.40m. A person (P) is at a distance of 2.40m. A person (P) is at a distance of 3.20m directly in front of one of the speakers as shown in Fig. 7.8. Find the frequencies in the audible range (20−20,000Hz) for which the listener will hear a minimum sound intensity . Speed of sound in air = 320 m//s.
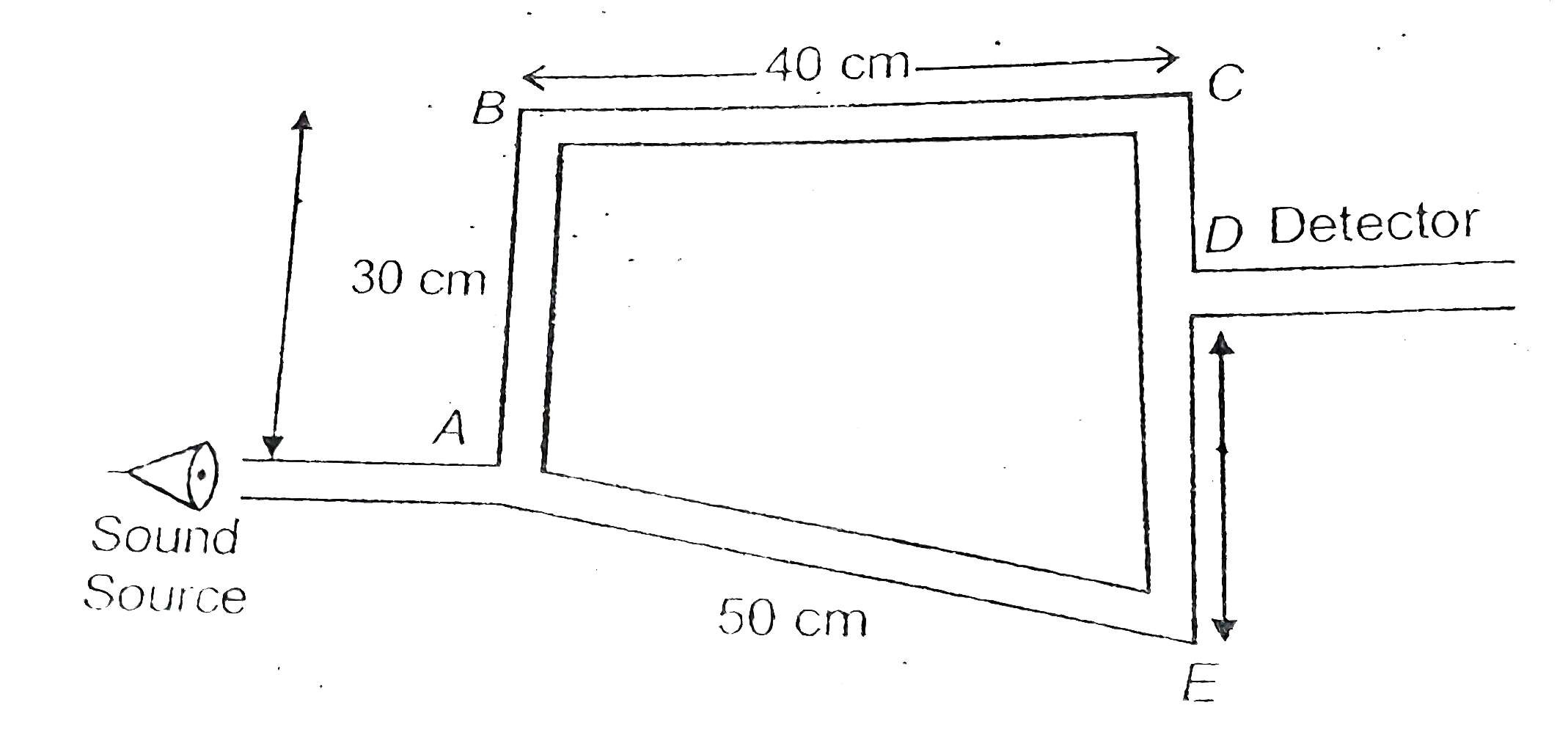
View SolutionIn the shown figure ABCDE is a tube which is open at A and D. A soruce of sound A is placed in front of A. if frequency of the source can be varried from 2000 Hz to 4000 Hz. Find frequencies at which a detector placed in front of D receives a maxima of intensity.
(Given speed of sound =340m/s)
View SolutionA siren emitting a sound of frequency 2000 Hz moves away from you towards a cliff at a speed of 8 m/s.
(a) What is the frequency of the sound you hear coming directly from the siren.
(b) What is the frequency of sound you hear reflected off the cliff. Speed of sound in air is 330ms.
View SolutionTwo trains are travelling towards each other both at a speed of 90kmh−1. If one of the trains sounds a whistle at 500 Hz, what will be the apparent frequency heard in the other train ? Speed of sound in air =350ms−1.
View SolutionA person is listening to a tone of 500Hz sitting at a distance of 450m from the source of the sound. What is the time interval between successive compressions from the source ?
View SolutionThe distance between the two identical speakers shown in Fig. 14.3.3 are 4.00m. They are driven by the same osicllator. Initially a listner stays at L at a distance 8.0 m from the centre of the line connecting the two speakers. The listner then walks to the point A where AL=0.4m. The first minium is sound intensity in heard just the listener reaches the point A. Find the frequency of the oscillator. Speed of sound in air is 340 m/s.
View SolutionAn electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air =320ms−1
View Solution
