A current I flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
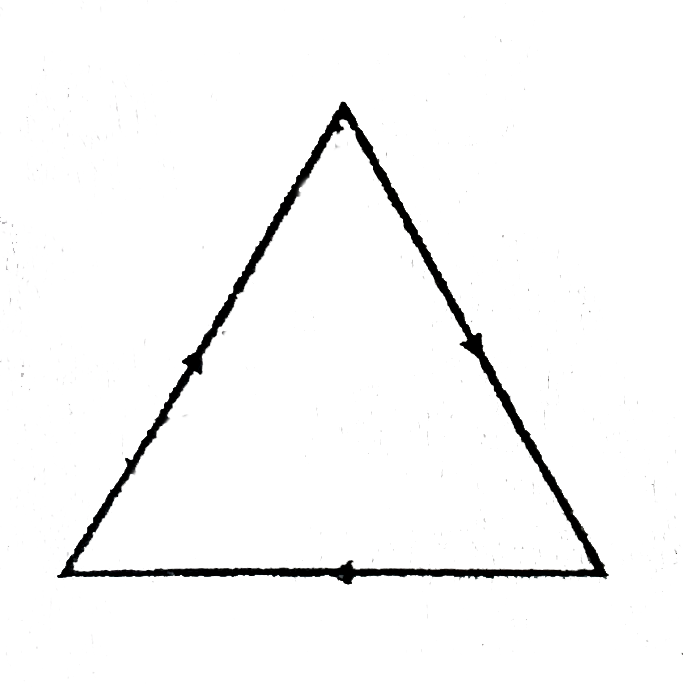
3μ0I2πa
9μ0I2πa
(3√3μ0I)/(2πa)
3μ0I4πa
The correct Answer is:B
The magnetic field at the cenetoid (or circumcentre) because of side AB of triangular loop is
μ04π=i(sin60∘+sin60∘)a2√3=3μ0I2πa

hence the net magnetic field due to all 3 sides is
3×9μ0I2πa
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 3
99 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View SolutionA current I flows along a round circular loop of radius R. Find the line integration of magnetic field along the axis of the loop from center to ∞
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionIn Fig. the conductors carry equal currents i. All straight segments are very long, and the two circular loops have equal radii. However, the currents around the loops have opposite sense. The ratio of the magnetic field at a and b, at the centres of the two loops, is
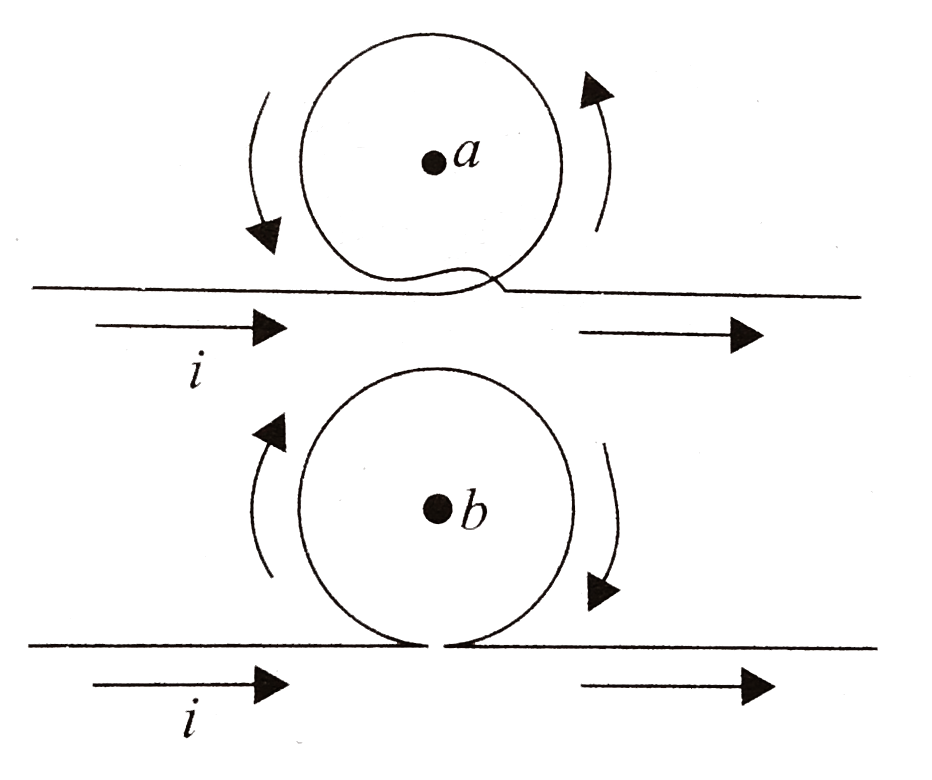
View SolutionA current loop in a magnetic field
View SolutionA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. it is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionA wire of length l carries a steady current. It is bent first to form a circular plane loop of one turn. The magnetic field at the centre of the loop is B. The same length is now bent more sharply to give a double loop of smaller radius. The magnetic field at the centre caused by the same is
View Solution