A box of mass resting on a frictionless horizontal ground is acted upon by a horizontal force F, which varies as shown. Find speed of the particle when force ceases to act.
To solve the problem step by step, we will use the concepts of momentum and the area under the force-time graph.
Step 1: Understand the Given Information
We have a box of mass m=2kg resting on a frictionless horizontal ground. A horizontal force F acts on the box, and we need to find the speed of the box when the force ceases to act.
Step 2: Analyze the Force-Time Graph
The force F varies with time as shown in the graph. We need to calculate the area under the force-time graph to find the impulse imparted to the box.
Step 3: Calculate the Area Under the Graph
Assuming the graph shows a triangular shape, we can calculate the area (impulse) as follows:
- The base of the triangle (time duration) = 4s
- The height of the triangle (maximum force) = 20N
The area A of the triangle can be calculated using the formula:
A=12×base×height
Substituting the values:
A=12×4×20=40Ns
Step 4: Relate Impulse to Change in Momentum
Impulse is equal to the change in momentum:
Impulse=Δp=pf−pi
Where:
- pf = final momentum
- pi = initial momentum
Step 5: Calculate Initial Momentum
Since the box is initially at rest:
pi=m⋅vi=2kg⋅0=0kg m/s
Step 6: Calculate Final Momentum
From the impulse calculated:
Δp=40Ns
Thus:
pf=pi+Δp=0+40=40kg m/s
Step 7: Calculate Final Velocity
Using the final momentum to find the final velocity:
pf=m⋅vf⟹40=2⋅vf
Solving for vf:
vf=402=20m/s
Conclusion
The speed of the box when the force ceases to act is 20m/s.
---
We have a box of mass m=2kg resting on a frictionless horizontal ground. A horizontal force F acts on the box, and we need to find the speed of the box when the force ceases to act.
The force F varies with time as shown in the graph. We need to calculate the area under the force-time graph to find the impulse imparted to the box.
Assuming the graph shows a triangular shape, we can calculate the area (impulse) as follows:
- The base of the triangle (time duration) = 4s
- The height of the triangle (maximum force) = 20N
A=12×base×height
Substituting the values:
A=12×4×20=40Ns
Impulse is equal to the change in momentum:
Impulse=Δp=pf−pi
Where:
- pf = final momentum
- pi = initial momentum
Since the box is initially at rest:
pi=m⋅vi=2kg⋅0=0kg m/s
From the impulse calculated:
Δp=40Ns
Thus:
pf=pi+Δp=0+40=40kg m/s
Using the final momentum to find the final velocity:
pf=m⋅vf⟹40=2⋅vf
Solving for vf:
vf=402=20m/s
The speed of the box when the force ceases to act is 20m/s.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A particle initially at rest on a frictionless horizontal surface, is acted upon by a horizontal force which is constant is size and direction. A graph is plotted between the work done (W) on the particle, against the speed of the particle, (v). If there are no other horizontal forces acting on the particle the graph would look like
View SolutionA wedge of mass M resting on a horizontal frictionless surface is acted upon by a force F in the horizontal direction as shown in figure. Find the net horizontal force acting on the shaded portion of the wedge.

View SolutionA wedge of mass M resting on a horizontal frictionless surface is acted upon by a force F in the horizontal direction as shown in figure. Find the net horizontal force acting on the shaded portion of the wedge.

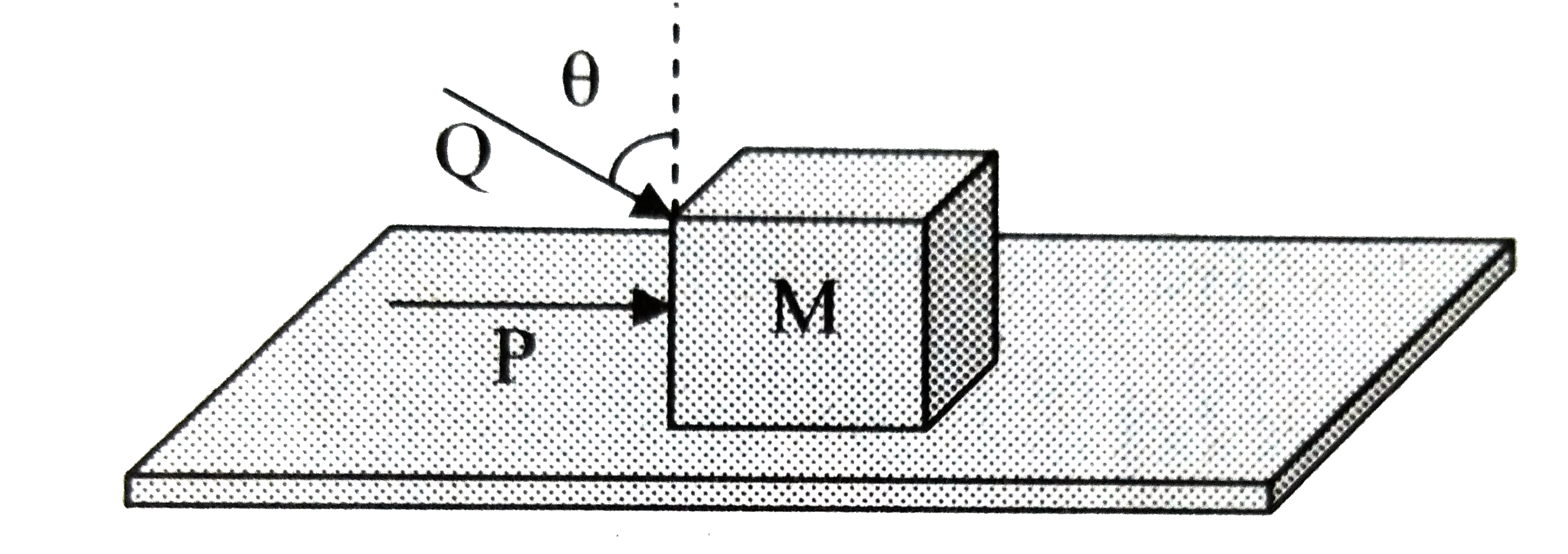
View SolutionA block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
View SolutionA particle at rest on a frictionless table is acted upon by a horizontal force which is constant in magnitude and direction. A graph is plotted of the work done on the particle W, against the speed of the particle v. If there are no frictional forces acting on the particle, the graph will look like
View SolutionA ball of mass m kept at the corner as shown in the figure, is acted by a horizontal force F. The correct free body diagram of ball is

View SolutionTwo forces F1 and F2 are applied simultaneously on a 2kg block resting on a frictionless horizontal ground. The forces vary with time according to graphs shown and cease to act after 8s. What maximum speed (inm/s) does the block acquire?

View SolutionA block of mass m=3kg resting on a horizontal frictionless flooe is horizontally struck by a 9N force that acts for 0.02 sec. After 3 sec it receivers a second blow of force 9 N but in opposite direction which acts for 0.01 sec. The speed of the body after 30 sec is
View SolutionA body of mass 5/6kg kept at rest in horizontal plane is acted upon by a variable force given by F=5e−1 newton in the same horizontal plane. Find the terminal velocity attained by the body.
View SolutionA body of mass 10 kg lies on a rough horizontal surface. When a horizontal force of F newtons acts on it, it gets an acceleration of 5m/s2. And when the horizontal force is doubled, it gets an acceleration of 18m/s2. The coefficient of friction between the body and the horizontal surface is
View Solution
