Two point masses m1 and m2 are connected by a spring of natural length l0. The spring is compressed such that the two point masses touch each other and then they are fastened by a string. Then the system is moved with a velocity v0 along positive x-axis. When the system reached the origin, the string breaks (t=0). The position of the point mass m1 is given by x1=v0t−A(1−cosωt) where A and ω are constants. Find the position of the second block as a function of time. Also, find the relation between A and l0.
The correct Answer is:x2=v0t+m1m2A(1−cosωt),l0=(m1m2+1)A
The string snaps and the spring force comes into play. The spring force beings an internal force for the two mass-spring system will not be able to change the velocity of centre of mass. This means the location of centre of mass at time t will be v0t
xcm=m1x1+m2x2m1+m2=v0t
⇒m1[v0t−A(1−cosωt)]+m2x2=v0tm1+v0tm2
⇒m2x2=v0tm1+v0tm2−v0tm1+m1A(1−cosωt)
⇒m2x2=v0tm2+m1A(1−cosωt)
⇒x2=v0t+m1m2A(1−cosωt)
(b) Given that x1=v0t−A(1−cosωt)
∴dx1dt=v0−Aωsinωt
∴d2x1dt2=−Aω2cosωt ....(i)
This is the acceleration of mass m1. When the spring comes to its natural length instantaneously then d2x1dt2=0 and x2−x1=l0
∴[v0t+m1m2A(1−cosωt)]−[v0t−A(1−cosωt)]=l0
(m1m2+)A(1−cosωt)=l0
Also when d2x1dt2=0,cosωt=0 from (1)
∴l0=(m1m2+1)A
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A20videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
The two masses m1 and m2 are joined by a spring as shown. The system is dropped to the ground from a height. The spring will be
 View Solution
View SolutionTwo particles of masses m1andm2 are connected to a string and the system is rotated in a horizontal plane with 'P' as center. The ratio of tension in the two parts of string is
 View Solution
View SolutionTwo masses m1andm2 re connected by a spring of spring constant k and are placed on as frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
View SolutionA particle of mass m is moving with constant velocity v0 along the line y=b. At time t=0 it was at the point (0,b). At time t=bv0, the
 View Solution
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionTwo blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shape impulse so that it acquires a velocity v0 towards right. Find a. the velocity of the centre of mass b. the maximum elongation that the spring will suffer.
 View Solution
View SolutionTwo beads of mass 2m and m, connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure )

If the rod is replaced by a massless string of length l and the system is released when the string is horizontal then :View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
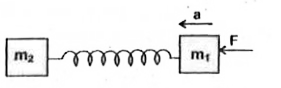
View SolutionTwo blocks of masses m1 and m2 are connected to each other with the help of a spring. If pushing force F is given to the mass m1 providing acceleration a to it, then acceleration of m2 is
 View Solution
View Solution

