The friction coefficient between the horizontal surface and blocks A and B are 115 and 215 respectively. The collision between the blocks is perfectly elastic. Find the separation (in meters) between the two blcoks when they come to rest.
The correct Answer is:5m
To solve the problem step by step, let's break it down:
Step 1: Understand the given data
- Coefficient of friction for block A, μA=115
- Coefficient of friction for block B, μB=215
- The collision between the blocks is perfectly elastic.
Step 2: Determine the initial conditions
Assume both blocks are moving towards each other before the collision. Let the initial velocity of block A be uA and block B be uB. For simplicity, let's say uA=4m/s and uB=0m/s (block B is at rest).
Step 3: Analyze the perfectly elastic collision
In a perfectly elastic collision, both momentum and kinetic energy are conserved.
1. Final velocity of block A after collision:
Since block A comes to rest after the collision, vA=0.
2. Final velocity of block B after collision:
Using the conservation of momentum:
mAuA+mBuB=mAvA+mBvB
Since vA=0:
mA(4)+mB(0)=mA(0)+mBvB
This simplifies to:
vB=mAmB⋅4
Assuming mA=mB (for simplicity), we have:
vB=4m/s
Step 4: Calculate the distance traveled by block B before coming to rest
Block B will experience friction and come to rest. The frictional force can be calculated as:
fB=μBmBg=215mB⋅10=43mB
Using Newton's second law, the acceleration aB (deceleration due to friction) is:
aB=fBmB=43
The distance x traveled by block B before coming to rest can be calculated using the kinematic equation:
v2B=u2B+2aBx
Substituting vB=0 (final velocity), uB=4m/s, and aB=−43:
0=(4)2+2(−43)x
This simplifies to:
0=16−83x
Rearranging gives:
83x=16⟹x=16⋅38=6m
Step 5: Find the total separation between the two blocks
Since block A comes to rest immediately after the collision and block B travels 6 meters before coming to rest, the total separation between the two blocks when they come to rest is:
Separation=x=6m
Final Answer:
The separation between the two blocks when they come to rest is 6 meters.
---
- Coefficient of friction for block A, μA=115
- Coefficient of friction for block B, μB=215
- The collision between the blocks is perfectly elastic.
Assume both blocks are moving towards each other before the collision. Let the initial velocity of block A be uA and block B be uB. For simplicity, let's say uA=4m/s and uB=0m/s (block B is at rest).
In a perfectly elastic collision, both momentum and kinetic energy are conserved.
Since block A comes to rest after the collision, vA=0.
Using the conservation of momentum:
mAuA+mBuB=mAvA+mBvB
Since vA=0:
mA(4)+mB(0)=mA(0)+mBvB
This simplifies to:
vB=mAmB⋅4
Assuming mA=mB (for simplicity), we have:
vB=4m/s
Block B will experience friction and come to rest. The frictional force can be calculated as:
fB=μBmBg=215mB⋅10=43mB
Using Newton's second law, the acceleration aB (deceleration due to friction) is:
aB=fBmB=43
The distance x traveled by block B before coming to rest can be calculated using the kinematic equation:
v2B=u2B+2aBx
Substituting vB=0 (final velocity), uB=4m/s, and aB=−43:
0=(4)2+2(−43)x
This simplifies to:
0=16−83x
Rearranging gives:
83x=16⟹x=16⋅38=6m
Since block A comes to rest immediately after the collision and block B travels 6 meters before coming to rest, the total separation between the two blocks when they come to rest is:
Separation=x=6m
The separation between the two blocks when they come to rest is 6 meters.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
The friction coefficient between the horizontal surfce and ech of the blocks shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g=10ms2.
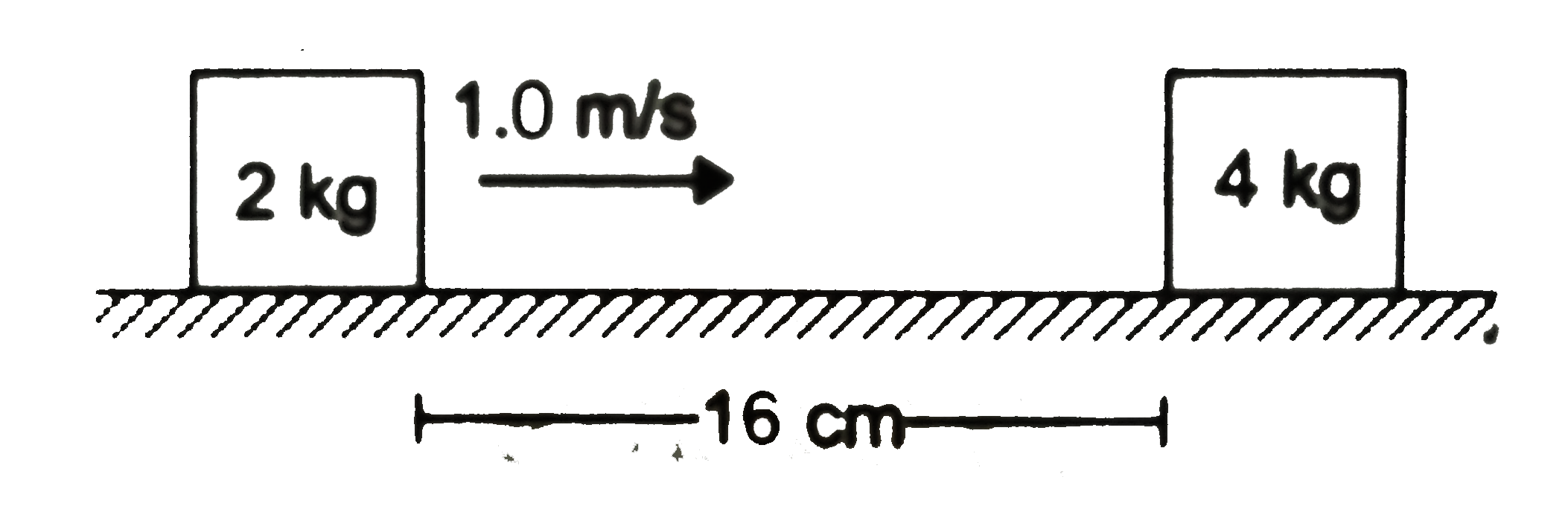
View SolutionThe friction coefficient between the horizontal surface and each of the block shown in the figure is 0.2. The collision between the blocks is perfectly elastic. Find the separation between them when they come to rest. (Take g=10m/s2).

View SolutionA small block of mass M moves with velocity 5 m/s towards an another block of same mass M placed at a distance of 2 m on a rough horizontal surface . Coefficient of friction between the blocks and ground is 0.25 . Collision between the two blocks is elastic , the separation between the blocks , when both of them come to rest , is ( g = 10m/s2)
View SolutionFor shown situation, if collision between block A and B is perfectly elastic, then find the maximum energy stored in spring in joules.
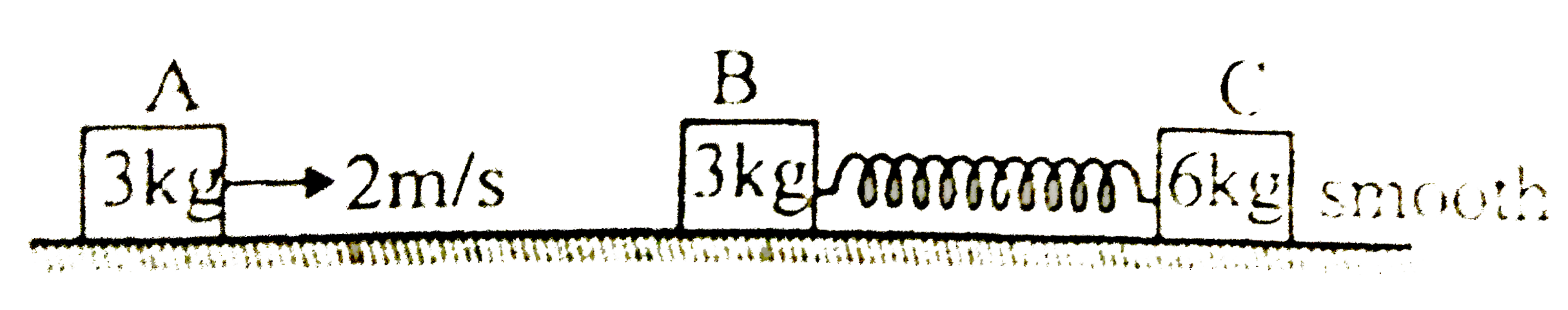
View SolutionTwo blocks of masses m and 3m on a horizontal surface are in contact with the ends of a horizontal massless spring. The coefficient of friction between m and surface and between 3m and surface is μ and μ/3 respectively. The two blocks are moved towards each other to compress the spring and then released. The two blocks move off in opposite directions covering distances S1 and S2 before comming to rest. S1:S2 is
View SolutionIn fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block

View SolutionBlock A has a mass 3kg and is sliding on a rough horizontal surface with a velocity uA=2m/s when it makes a direct collision with block B, which has a mass of 2kg and is originally at rest. The collision is perfectly elastic. Determine the velocity of each block just after collision and the distance between the blocks when they stop sliding. The coefficient of kinetic friction between the blocks and the plane is μk=0.3 ( Take g=10m/s2)
View SolutionTwo blocks A and B each of mass m are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on blocks A and B, respectively, as shown in fig. Block A does not slide on block B. Then then the normal reaction acting between the two blocks is (assume no friction between the blocks)
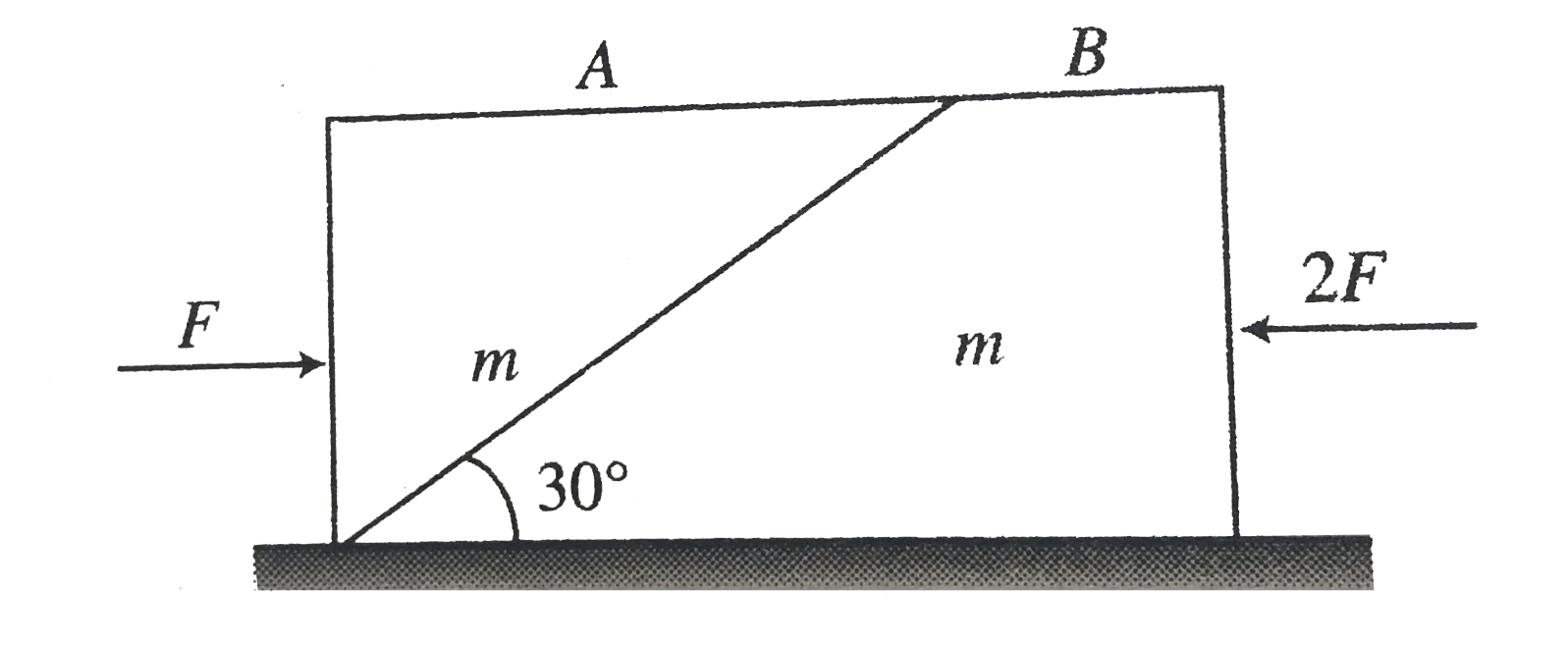
View SolutionTwo blocks A and B each of mass m are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on blocks A and B, respectively, as shown in fig. Block A does not slide on block B. Then then the normal reaction acting between the two blocks is (assume no friction between the blocks)

View SolutionTwo blocks A and B each of mass m are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on blocks A and B, respectively, as shown in fig. Block A does not slide on block B. Then then the normal reaction acting between the two blocks is (assume no friction between the blocks)

View Solution
