Question

A particle of mass m, kinetic energy K and momentum p collides head on elastically with another of mass 2 m at rest. Match the following columns after collision.)
$\begin{array}{cc}\text{column1}& \text{column2}\\ \text{A momentum of first particle}& \text{P 3/4 p}\\ \text{B Momentum of second particle}& \text{Q -K/9}\\ \text{C Kinetic energy of first particle}& \text{R -p/3}\\ \text{D Kinetic energy of second particle}& \text{S 8K/9}\end{array}$

Answer

(A) `rarr` r; (B) `rarr` t; (C ) `rarr` t; (D) `rarr` s

Explanation

By applying conservation of momentum

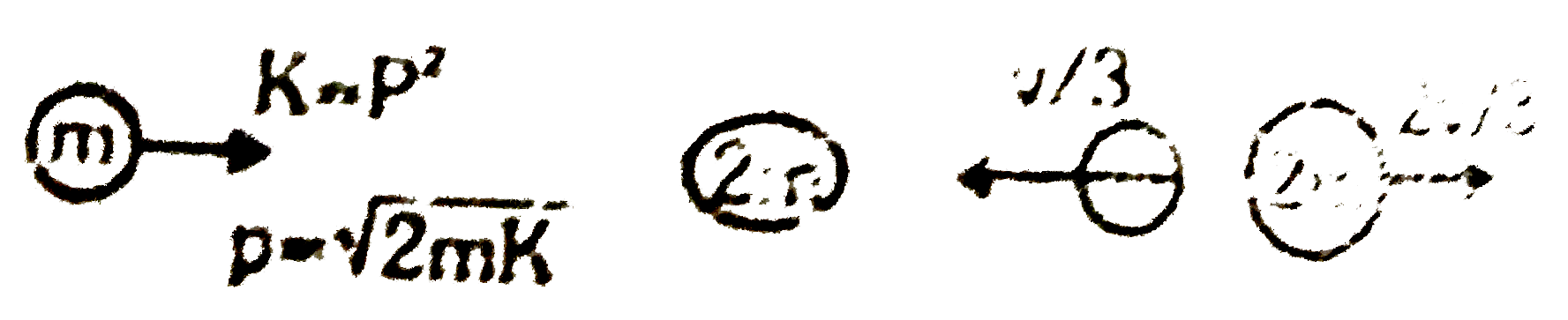
`m_(1)u_(1) + 2m(0) = mv_(1) + 2mv_(2)` …..(i)
Also `u = v_(2) - v_(1)` …….(ii)
`v_(2) = (2v)/(3)` and `v_(1) = -(v)/(3), F_(2) = (4mv)/(3) = (4p)/(3)`,
`P_(1) = -(mv)/(3) = -(P)/(3), K_(2) = (8K)/(9), K_(1) = (K)/(9)`